七.运算放大器

七.运算放大器

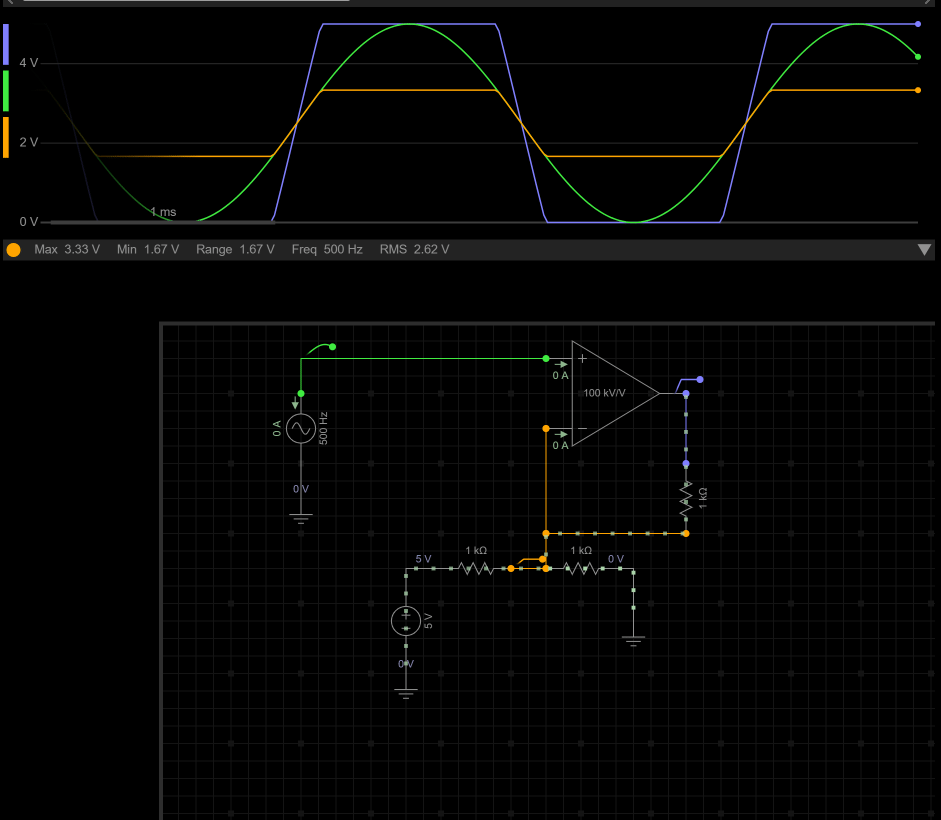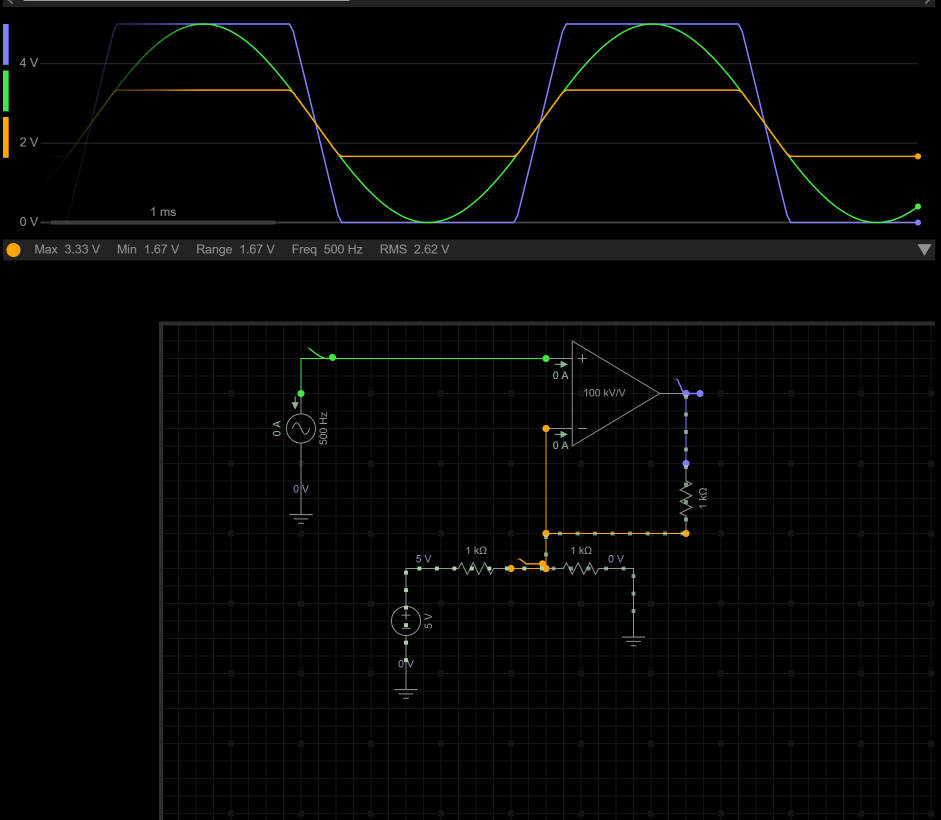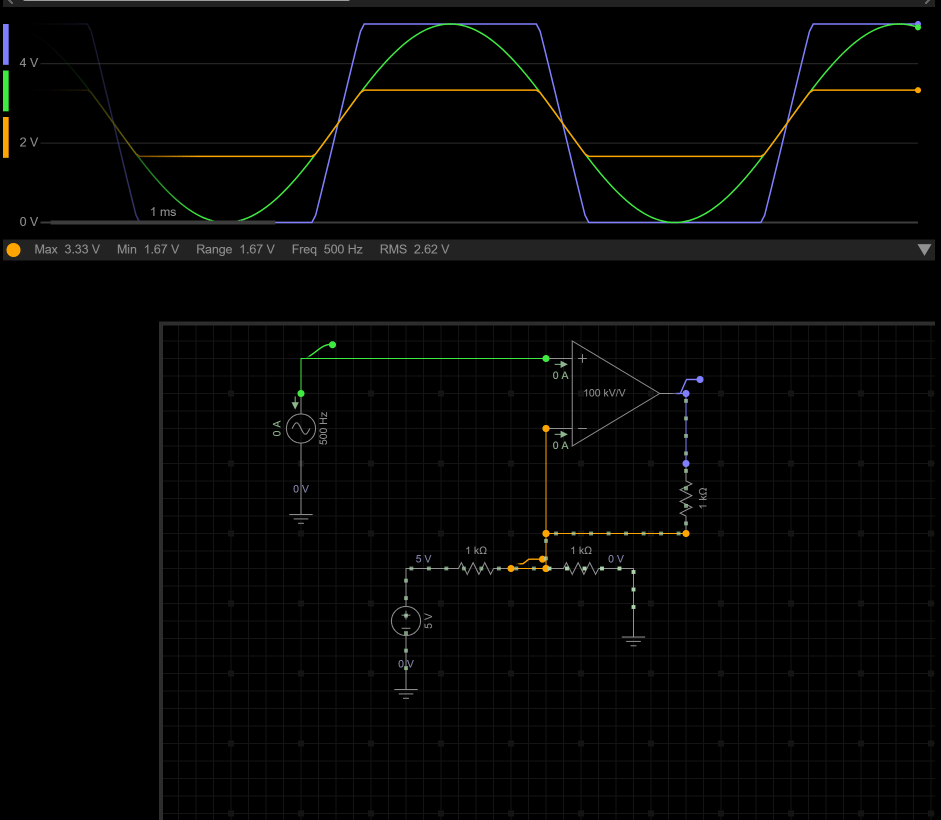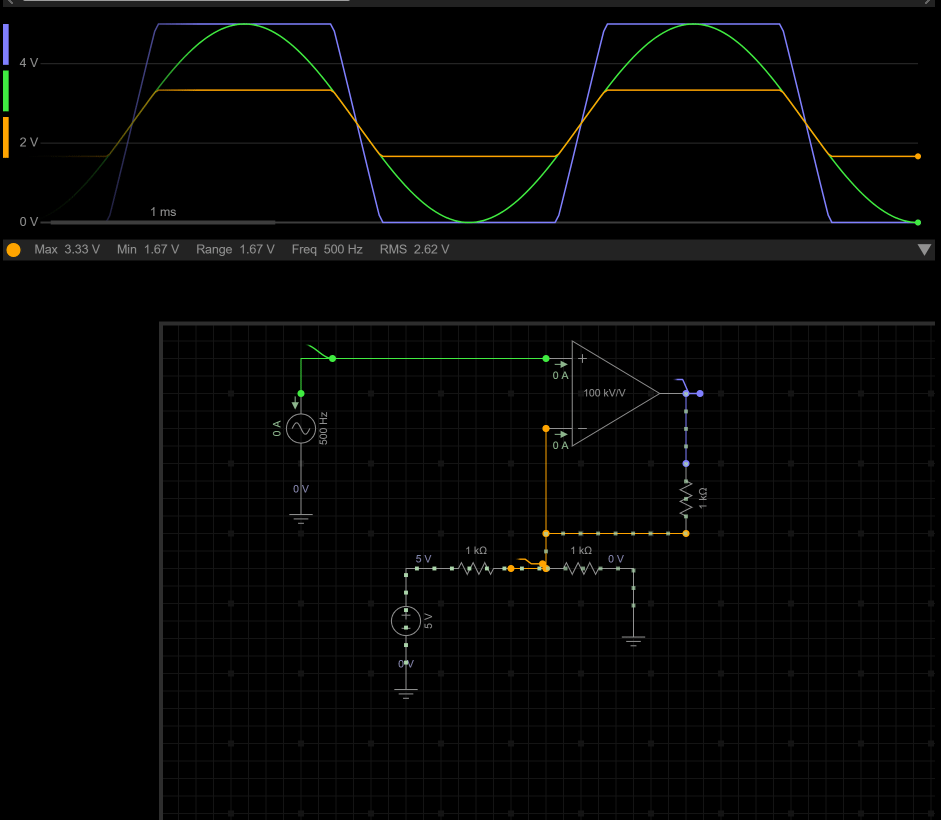
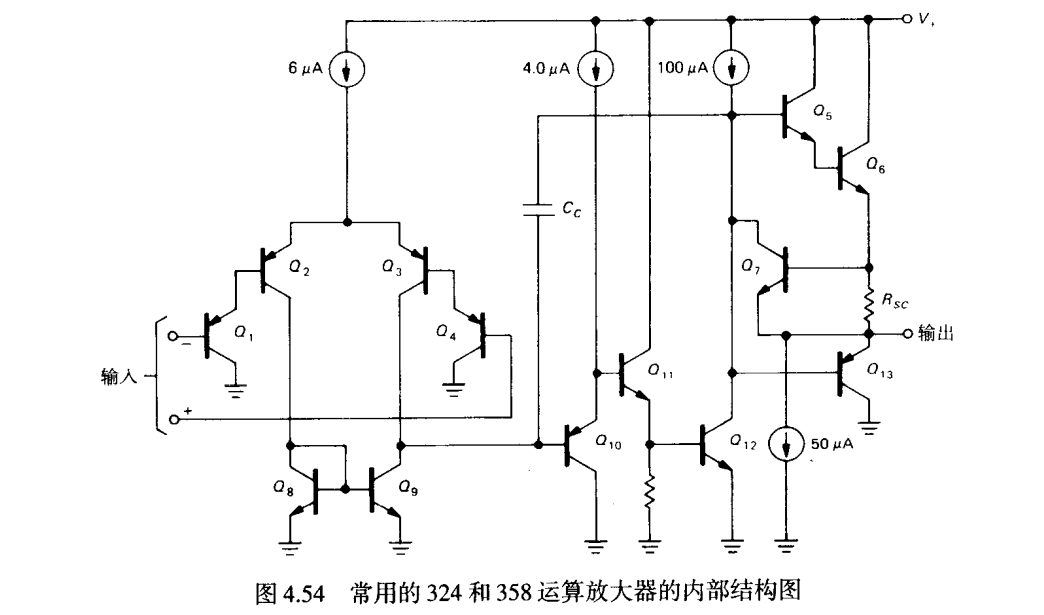
一.运算放大器基础

反馈简介

将输出耦合回输入,并抵消部分输入

降低增益

改善了失真和非线性

响应的平坦度(符合期望的频率响应)

用处

如果反馈特性和频率相关,可构成均衡放大器(RIAA音频放大)

和幅度相关,构成非线性放大器(对数放大器)

可以得到 电流源 电压源

正反馈可以构成振荡器(避免震荡需要"补偿"技术)

运算放大器设计准则

黄金准则: V−=V+且有Iin=0V_-= V_+ 且有 I_{in}=0V−​=V+​且有Iin​=0﻿

在黄金准则下,不能看似V+ V−V_+\  V_-V+​ V−​﻿为等效的,但是不能将二者弄混

必须有直流反馈,否则运放讲进入饱和状态(即考虑输入偏置电压)

同向放大器:

结构图解: 输入接入V−V_-V−​﻿,考虑开环下输出与输入相反,所以输出反馈到V−V_-V−​﻿

缺点: Zin=R1Z_{in}=R_1Zin​=R1​﻿ 有点小(由于V+V_+V+​﻿直接接地,则有V−V_-V−​﻿相当于虚地,可当地运算)

反向放大器

结构图解: 输入接入V+V_+V+​﻿,考虑开环下输出相同,所以输出反馈到V−V_-V−​﻿

当信号交流耦合时候,需要为极小的输入电流提供到地的回路(???为何,输入阻抗不是越高越好么?)

可能因为考虑RC时间常数,如果RC过大,则有电压变化时间无限大,电压基本不变,所以需要并联R减小时间常数.

跟随器: 

具有良好的隔离特性,低输出阻抗,高输入阻抗,也称缓冲器

二.电流/电压源

电流源

一般形式

简单形式

缺点: 负载悬空,无法使得负载的某一端确认接地

悬空电路法

将电路整个悬空,输入V_{+} V_{-}的电压差通过一个类似电池的东西提供

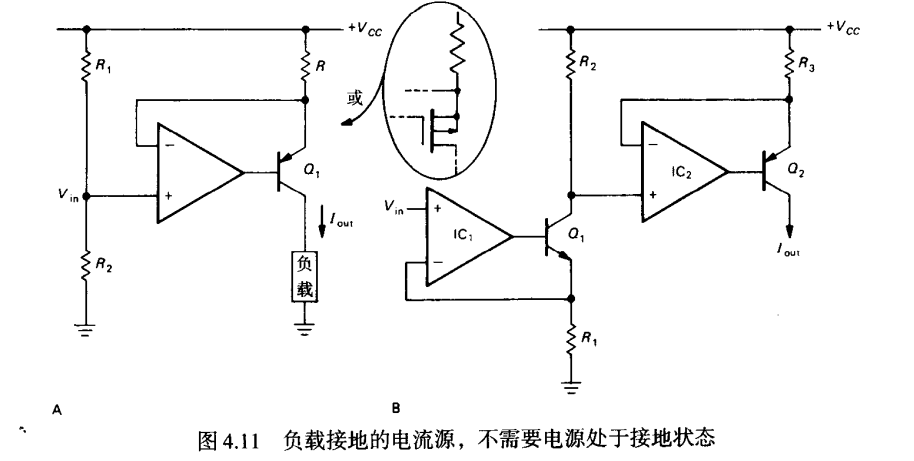
BJT输出级电流源

负载接地电流源形式

左边电路,输出电流为(VCC−VIN)/R(V_{CC}-V_{IN})/R(VCC​−VIN​)/R﻿

非理想因素

BJT部分基极电流IbeI_{be}Ibe​﻿ 使得IOUT≠IRI_{OUT} ≠ I_RIOUT​=IR​﻿

运放的偏移电压V_{OS} 使得 VINV_{IN}VIN​﻿需要补偿偏移的部分

负载接地-V_{IN}参加计算

VINV_{IN}VIN​﻿不是直接参加计算的量,而是和VCCV_{CC}VCC​﻿的差值

为何不直接用左半部分的电路,即将R2R_2R2​﻿变成负载?—-R2R_2R2​﻿不接地

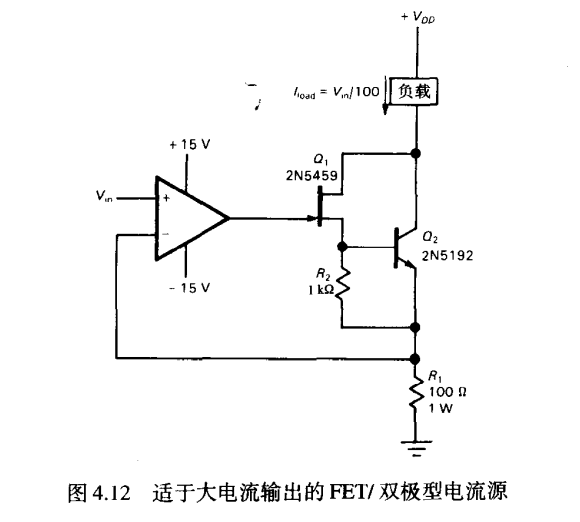
JFET-BJT输出级运放电流源

JFET-运放电流源

优点: 无基极电流的影响

为何Q2Q_2Q2​﻿并联R2R_2R2​﻿

回忆达林顿连接: 电阻R防止漏极电流使得Q2Q_2Q2​﻿导通

回忆FET源级跟随器有源负载: 

Howland电流源

...

三种电流源的本质思考

JFET-运放电流源

BJT FET 运放电流源

都是通过一个跟随器取样电压: 对运放而言是V-=V+,对BJT而言是V_B=V_E

然后制造一个可计算的回路,跟随器输出口电流既不输入也不输出,只用作电压锚点

对于三端口电流,若锚定两端即确定了电流,由于跟随器输出口端无电流,即制造了一个电流源

可修改R1来修改电流大小

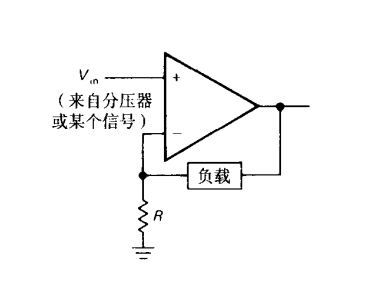
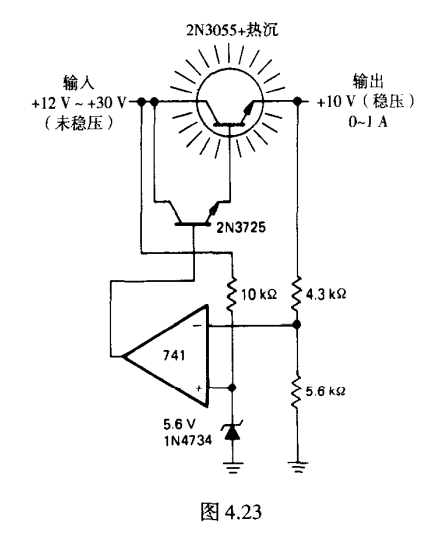
运放电压源

BJT输出级电流源

BJT互补输出级电流源

BJT-BJT达林顿输出级电压源

三种电压源的本质思考

跟电流源一样,核心也是一个跟随器取样电压

但是跟随器的输出直接接负载,或或者通过以一个分压器结构升压

电流通过输出级控制提供

三.整流/峰值检波/采样 (二极管-运放)

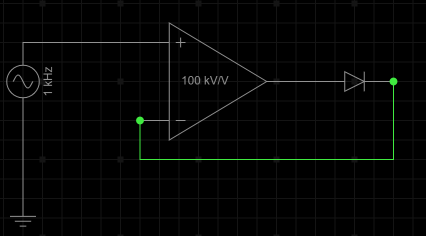
1.整流电路

精密半整流电路

精密整流-高阻电路

当Vin>0VV_{in}>0VVin​>0V﻿时候Vout=VinV_{out}=V_{in}Vout​=Vin​﻿

当Vin<0VV_{in}<0VVin​<0V﻿时候Vout=V_{out}=Vout​=﻿高阻态

这类二极管-运放电路如何分析

二极管不仅表示电压方向,也表示了电流方向.

当V_+>V_-时候,V_out为+,二极管可导通

当V_+<V_-时候,V_out为-,二极管不可导通

可通过此特性为正电压负电压设计不同的反馈回路

精密半波整流电路

整流-高阻+下拉电阻电路

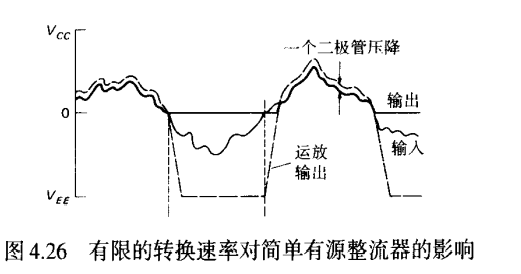
不同反馈回路 反向绝对值电路

可通过一个简单的下拉电阻,使得 整流-高阻电路 在V_{in}<0时候输出0V

Vin/Vout图

优点: 此类整流不受到二极管压降的影响

缺点: 此时运放开环工作输出为最大负电压,切换时候被Slew Rate限制

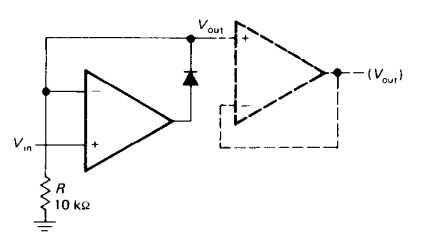
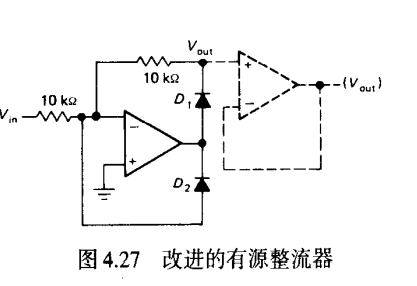
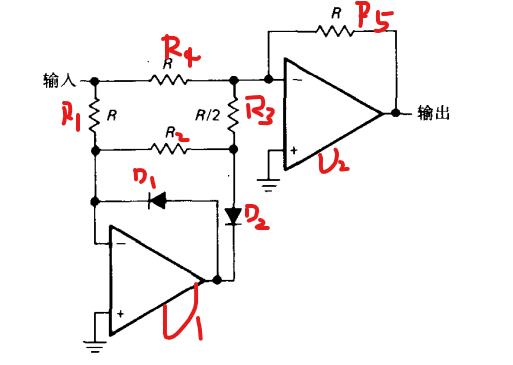
绝对值全波整流电路

绝对值全波整流器

当输入正电压

由于V−>0V_->0V−​>0﻿ 运放Vo<0V_o<0Vo​<0﻿ D1D_1D1​﻿断路

下面的U1U_1U1​﻿运放,和R2R_2R2​﻿,R1R_1R1​﻿一同单位反相器(此时有无D_2不影响,因为D_2只作为反馈回路选择器),使得D_2上方点位为−Vin-V_{in}−Vin​﻿

R4R_4R4​﻿,R3R_3R3​﻿构成一个加法器

当输入负电压

R_1下方点被钳位于0,相当于跨在两个电压源中间,对整体电路无影响,可删除,D2D_2D2​﻿断路

R_4,R_5构成了一个加法器 

2.有源峰值检波

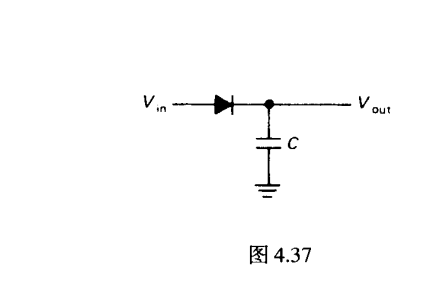
无源形式

无源峰值检波

对<0.6V电压不敏感 对>0.6V电压不精确

输入阻抗不断改变(不同f),导致输入电流不断变化,而且二极管压降取决于温度和电流

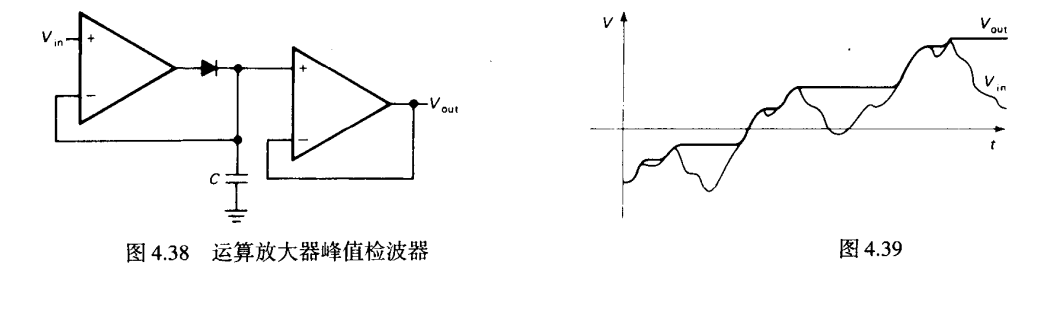
运放峰值检波

运放检波

Slew Rate有限: 当输入小于上次输出时候,运放工作在负饱和状态,下次超过输出的时候,运放需要Vout−V−/SRV_{out}-V_{-}/SRVout​−V−​/SR﻿ 来转换

运放输出电流有限: 由于ΔV=1C∫0tI\Delta V=\frac{1}{C} \int_0^t IΔV=C1​∫0t​I﻿ 输出电流有限也限制了电容变换速率(输出转换速率)

倾斜现象: 输入偏置电流导致对电容的慢放电或充电,最好选择高输入阻抗放大器(低偏置电流)即FET类型

二极管漏电流现象: 运放工作在负饱和状态,二极管反向电压较大,二极管会存在漏电流

峰值检波关键参数: 输出转换速率(受SR 输出电流大小 电容大小) 倾斜速率(受偏置电流影响),通常用二者比值衡量好坏,越高越好

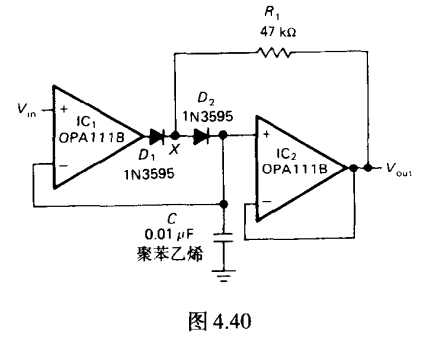
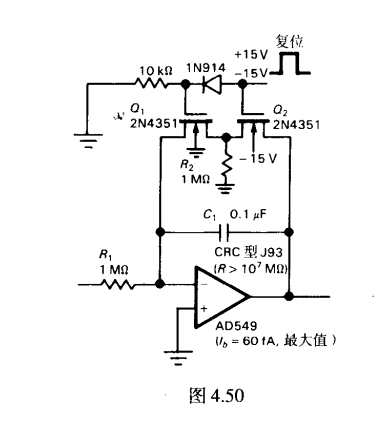
二极管漏电流改进 运放峰值检波

二极管改进峰值检波

如果采用了低输入电流的运放(0.01pA),则误差来到了二极管漏电流

当输入小于之前检测到的峰值时候,通过一个大电阻,使得D2两端反向压差减小,减小了漏电流

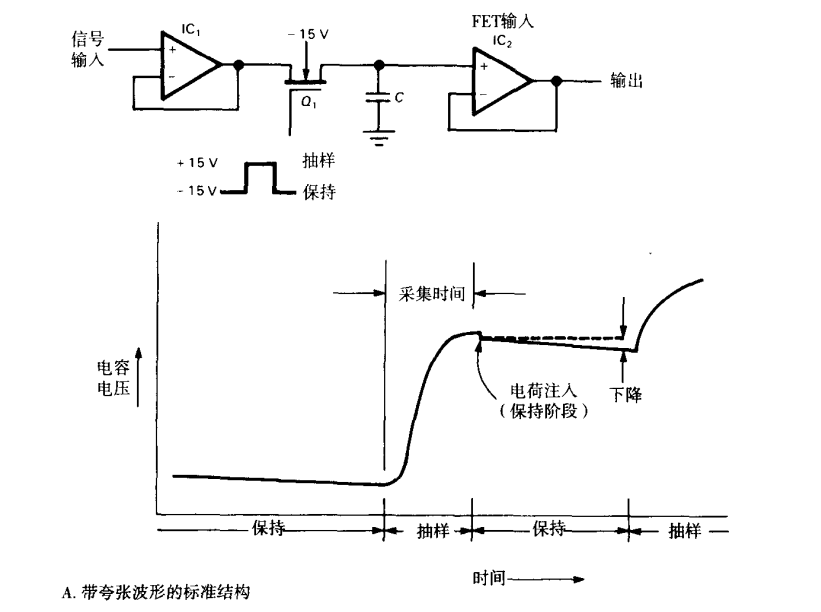
3.Sampling-Hold 采样保持电路

简易的采样保持电路及其标准结构

C选择取舍问题

保持时刻

在保持期间: dVdt=I漏电C\frac{dV}{dt}=\frac{I_{漏电}}{C}dtdV​=CI漏电​​﻿的速率下降,希望下降缓慢,可以增大C或减小漏电流

: 可以利用上面二极管漏电流改善的原理否?

采样时刻

由于R_ON/ESR存在,构成一个低通滤波器,R_ON越大,需要采样时间(τ=RC\tau=RCτ=RC﻿)越长,等效的,对于高频来说需要快采样

同时采样时刻输出变化速率同时受到SRate ,输出电流影响(分析见上面运放有源检波)

运放的容性负载问题

可能会不稳定(???)

可以选用专门驱动容性负载的运放LF355/6(0.01μ\muμ﻿F)

或者选用专门S/H IC 如: LF398 AD585(内部电容 跟随10V阶跃时间为3μ\muμ﻿s)

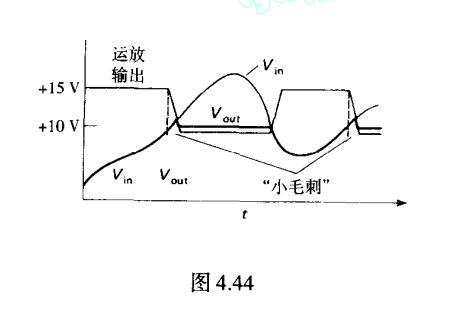
4.有源钳位

有源钳位电路

有源钳位"毛刺"

当Vin<10VV_{in}<10VVin​<10V﻿,二极管开路的时候Vout=VinV_{out}=V_{in}Vout​=Vin​﻿,此时运放工作于正饱和状态

当Vin>10VV_{in}>10VVin​>10V﻿时候,反馈回路接通Vout=10VV_{out}=10VVout​=10V﻿

当切换状态时候运放从正饱和→10V,有限的SlewRate导致细小的毛刺

三.放大器

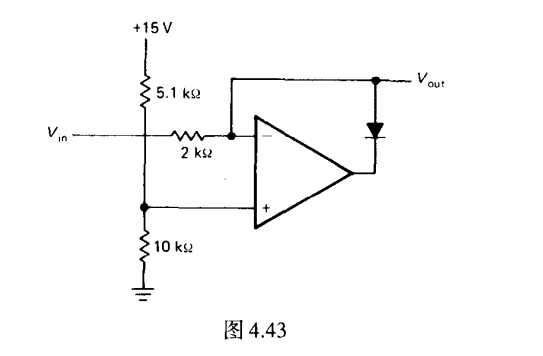
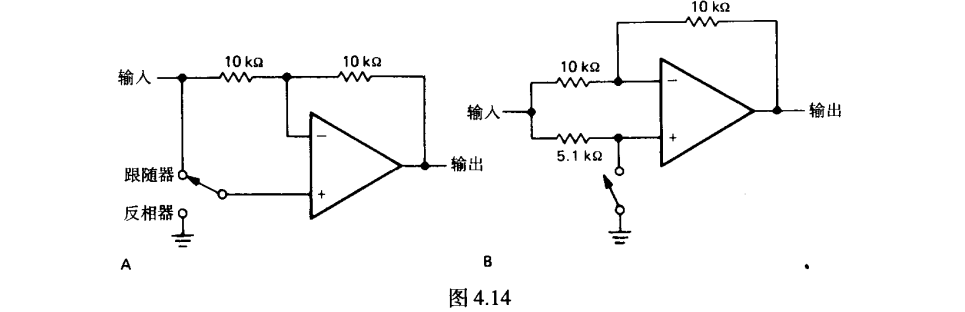
跟随器-反相器选择电路

跟随器反相器原理图

左图利用续断左边10K电阻

右图为使得5.1K电阻为同电源的无关电路

理想电流电压转换器(跨阻元件)

利用了虚地时候,输入电阻可以为0的特性

...

简易减法器(差分放大器)

RIAA均衡运算放大器

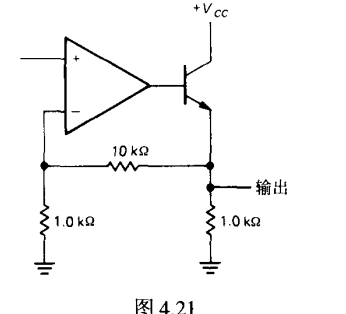
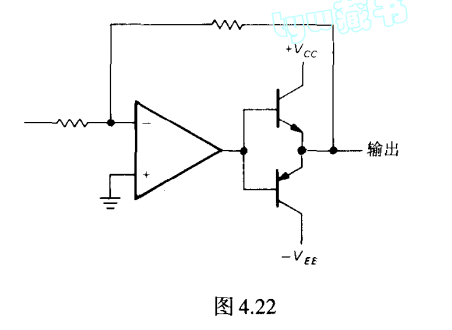
功率放大器

功率放大: 即可输出大电流的跟随器

电压增益为1,但是原来电路能输出电流很小,转换之后可以变得很大

推挽改进...

四.运算器

对数运放器

对数放大器原理: 三极管中IC I_CIC​﻿和VBEV_{BE}VBE​﻿为精确的指数关系 ICI_CIC​﻿增大10倍数,VBEV_{BE}VBE​﻿增大60mV

积分器

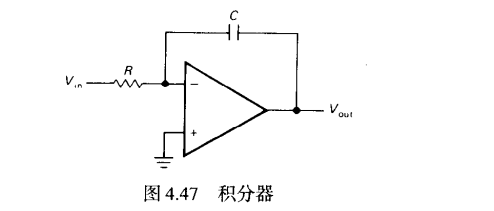
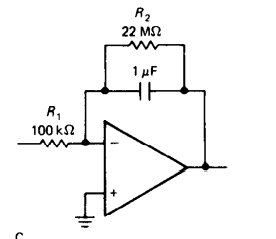
运放积分器

对于RC积分器而言,Vout=1C∫0t0Idt=1C∫(Vin−Vout/R)dtV_{out}=\frac{1}{C} \int_0^{t_0}I{dt} =  \frac{1}{C} \int(V_{in}-V{out}/R){dt} Vout​=C1​∫0t0​​Idt=C1​∫(Vin​−Vout/R)dt﻿ 当Vout<<VinV_{out}<<V_{in}Vout​<<Vin​﻿时候才能成立,R要增大或C增大

对于运放积分器而言 Vout/R=−C(dVout/dt)V_{out}/R=-C(dV_{out}/dt) Vout​/R=−C(dVout​/dt)﻿ 得 Vout=−1RC∫Vindt+常数V_{out} = -\frac{1}{RC} \int V_{in} dt + 常数Vout​=−RC1​∫Vin​dt+常数﻿

缺陷: 没有直流反馈,失调和偏置电流(失调电压) 导致运放输出漂移

解决缺陷思路 

本质上是V_{diff} 和虚地,电阻构成的电流源造成的

可以用较大的R来减少电流,或较大的C减缓漂移

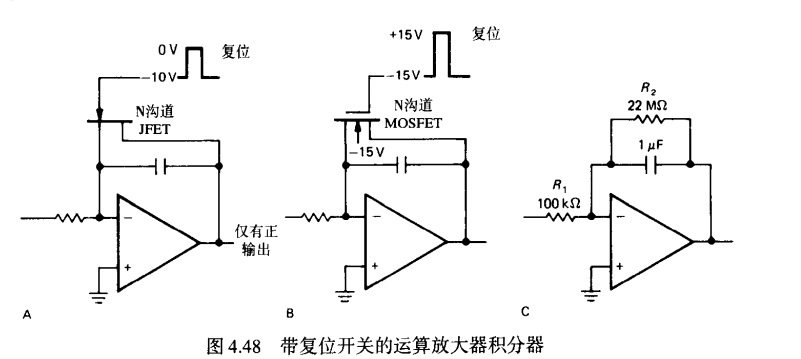
缺陷解决方法

快速置零法

周期性开关复位的积分器

由于电容将被周期性置零,短时间的便宜无影响

若失调电压25mV R=10M C=10μ\muμ﻿F 则1000s产生 0.003的漂移

构造直流反馈

大电阻直流反馈

通过大电阻回接到VINVV_{INV}VINV​﻿端口

为何不使用V−V_-V−​﻿代表反向输入端: 同负电源混淆

低频下(f<1/R2Cf<1/R_2 Cf<1/R2​C﻿)情况下积分器作用下降(时域分析):

I2R=1C∫I1dtI2+I1=Vin/R=I总I_2 R = \frac{1}{C} \int I_1 dt \\
I_2 + I_1 = V_{in}/R = I_总I2​R=C1​∫I1​dtI2​+I1​=Vin​/R=I总​﻿

变换后可得
Vout=1C∫(I总−I2)dtV_{out} = \frac{1}{C} \int (I_总-I_2) dtVout​=C1​∫(I总​−I2​)dt﻿

I2I_2I2​﻿越小表现越好,一开始,电容近似短路,表现良好

频率越低,电容充电时间越长,则I2I_2I2​﻿越大,积分效果越差

是否可以搭建一个镜像电流源,对电容进行补偿?

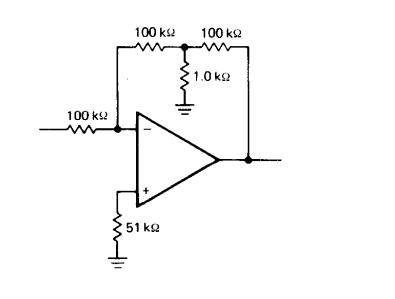
大电阻带来的杂散电容

电流源+电压源的T型网络放大

本质上是一个跨阻结构,可以通过T型网络来进行放大

避免直接采用一个

两种方法的结合

快速置零+大电阻直流反馈

微分器

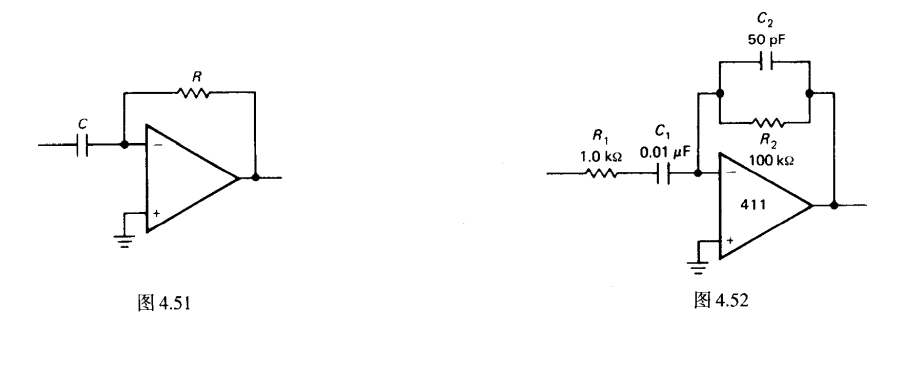
带滚降的微分器

直流偏置是稳定的

当由于运放的高增益和内部相移动,一般有噪声和高频不稳定性(???)

所以需要滚降微分器的作用(???)

高频区域由于R_1 C_2该电路变成了积分器(???只能用频域s参数分析么?)

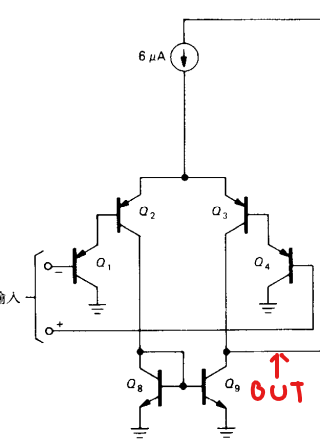
五.单电源运放(Rail to Rail)

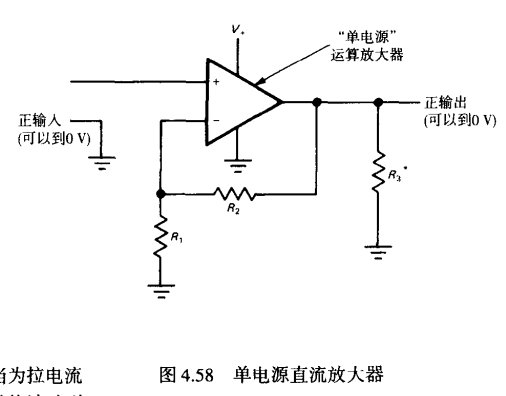
单电源运放: 指输入一直可以到地,输出却不一定,需要按情况分类

输入部分

PNP输入结构: 输入可以到GND负0.3V

LM324输入部分分析

分析

对于PNP管而言,Emitter端必须比Base端大

但是Collect不一定比Base端小

考虑VBE(sat)=0.7VV_{BE(sat)}=0.7VVBE(sat)​=0.7V﻿ VBC(sat)=0.3VV_{BC(sat)}=0.3VVBC(sat)​=0.3V﻿只需要BC不导通即可

即VB>0−0.3VV_B>0-0.3VVB​>0−0.3V﻿ 即可

为何输入级不能进入包河区同输出级不同,输入级进入饱和区时候,三极管相当于固定阻值的小电阻,无法检测到输入

该结构器件:

LM324/358 LT1013 TLC270 精确LT1006/LT1014 微功耗OP20/90

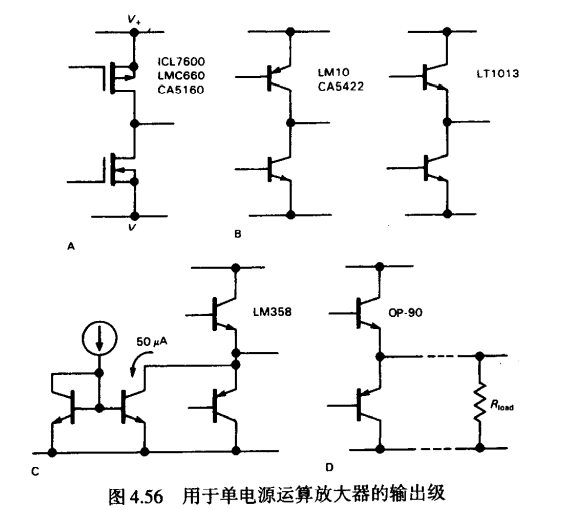
 输出部分

单电源输出级结构

几乎所有单电源运放都可拉电流到GND 灌电流到VCC

互补CMOS结构

典型器件: LMC660 CA5160 ICL76xx

可以做到真正的端到端,饱和输出的时候,MOS管相当于小电阻

互补BJT结构

典型器件: LM10 CA5422

分析同上,也是可以做到真正的端到端

VCE(sat)V_{CE(sat)}VCE(sat)​﻿不是最小压降为0.4V么,为何可以做到端到端

V_CE(sat)指的是工作在放大模式下的最小压降

对于输出级而言,放大饱和模式下依然算是可以工作的,复杂的协调交给负反馈去做

这同VBE(sat)>0.7VVC>VEV_{BE(sat)}>0.7V\quad V_C>V_E VBE(sat)​>0.7VVC​>VE​﻿这两个硬性条件不同,这个条件如果不满足的话,三极管无法工作

互补BJT不像推完BJT一样,上下BJT Base端可以接同样的信号,否则上下管直接自我导通

推挽BJT+灌电流补偿

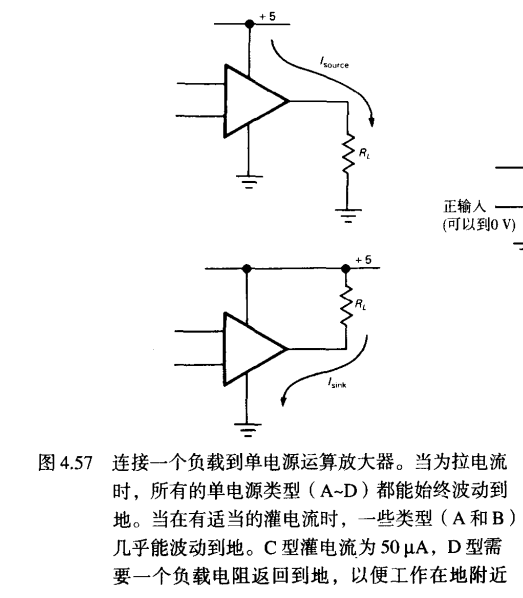
原则上推挽结构做不到GND(VBE(sat)>0.7VVC>VEV_{BE(sat)}>0.7V\quad V_C>V_EVBE(sat)​>0.7VVC​>VE​﻿) 两个强制条件

做不到GND是指灌电流做不到,如果是拉电流,由上管提供,是可以到GND

当需要输出灌电流地的时候,通过电流源接地,此时灌电流只能到50μ\muμ﻿A

(1型放大器)外围电阻补偿

1型放大器

对于部分无法灌电流到地的情况,可通过一个外围的上下拉电阻补偿A

六.开环/正反馈 运用

功率开关驱动器

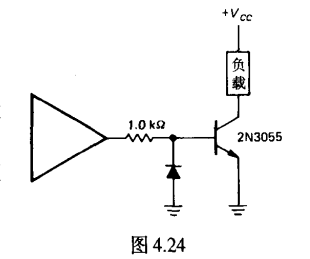
功率开关驱动器

简易的数字逻辑连接

注意加入稳压管防止反向击穿

比较器

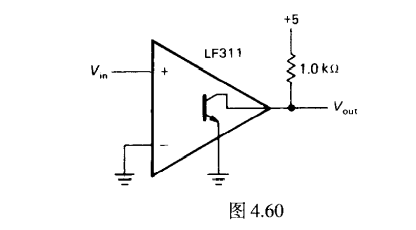
比较器精简输出级

LF311输出级示意图

本质上比较器只是运放的开环运用(正反馈),但比较器只是数字逻辑

不需要考虑电流的输出能力

也不需要考虑除VCC GND以外其他电平

一个简单上拉电阻+三极管开关便足够使用

专用比较器

比较器转换速率(Slew Rate): NE531可达 KV/s 

比较器中一般不使用Slew Rate而是使用propagation delay versus input overdrive 传播时延与输入过驱(???)

常见型号: LM306 LM311 LM393 NE572 TLC372

其他注意事项

无负反馈意味着放大器输入内阻没有被自居到很大的值(???) 放大器内阻不是有可能变小么?

有可能只允许有限的差分输入

施密特触发器

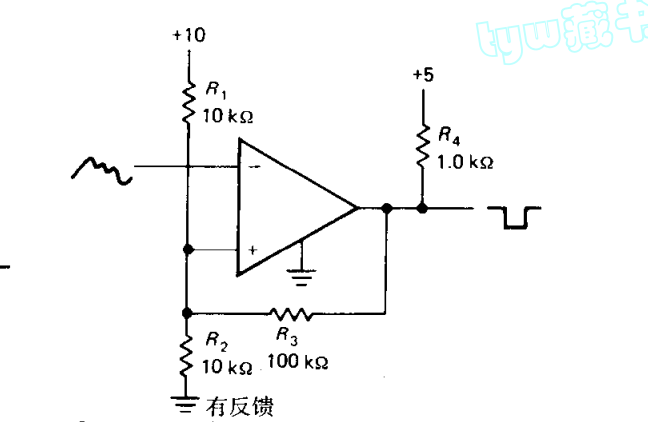
施密特触发器

分析

三端分压器

可以想象成一个三端分压器,其中一端为VCC GND两态可变

当输出为VCC时候,等效为R3并联到高端口,降低了阈值

当输出为GND时候,等效为R3并联到高端口,提高了阈值

接入VINVV_{INV}VINV​﻿分析或者输出通过反相器反馈到NONEINV端

反向端施密特仿真

反向端施密特仿真

中间有一段区域进入反馈状态,使得比较器意义丧失

成立的区间条件: 

实际角度: 在有限的输出电压下,调整输出电压使得VINV=VNOINVV_{INV}=V_{NOINV}VINV​=VNOINV​﻿

计算角度: 假设VINV=VNOINVV_{INV}=V_{NOINV}VINV​=VNOINV​﻿ 计算输出,查看输出是否在VCC-GND

或者直接将带入输出为VCC-GND带入计算出两个端点电压,中间区域即为线性区,与与通常施密特触发器的表现区别就在于门限区域为线性区

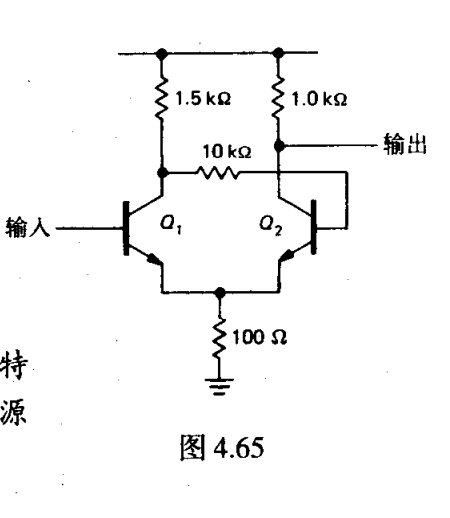
BJT分立结构

分立结构的施密特

分析(???)

仍然以设共模输入为VcmvV_{cmv}Vcmv​﻿ 差模输入±Vdif\pm V_{dif}±Vdif​﻿ 共模增益A 差模增益B

则有表达式 Vcmv−Vdif=A∗Vcmv+B∗VdifV_{cmv}-V_{dif} = A*V_{cmv} + B*V_{dif}Vcmv​−Vdif​=A∗Vcmv​+B∗Vdif​﻿

VdifVcmv=1−AB+1\frac{V_{dif}}{V_{cmv}} = \frac{1-A}{B+1}Vcmv​Vdif​​=B+11−A​﻿ 

七.反馈参数分析

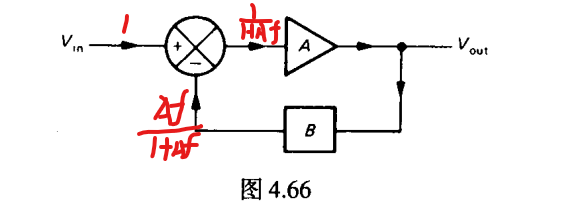
反馈增益 环路增益 反馈深度

反馈框图

Vout=A(Vin−fVout)V_{out}=A(V_{in}-fV_{out})Vout​=A(Vin​−fVout​)﻿ 两端同时除VinV_{in}Vin​﻿ 可得

GV=A(1−AfAf+1)=AAf+1G_V = A(1-\frac{Af}{Af+1})= \frac{A}{Af+1}GV​=A(1−Af+1Af​)=Af+1A​﻿

Af为环路增益 Af+1称作反馈深度

各参数的直观理解(反馈的通用计算基础)

现在 Af物理意义很显然: Af=1*Af即不加入求和点(无负反馈)下的增益(经过B)

1Af+1=1−AfAf+1\frac{1}{Af+1} = 1 - \frac{Af}{Af+1}Af+11​=1−Af+1Af​﻿ 等于经过求和之后的放大器A实际输入

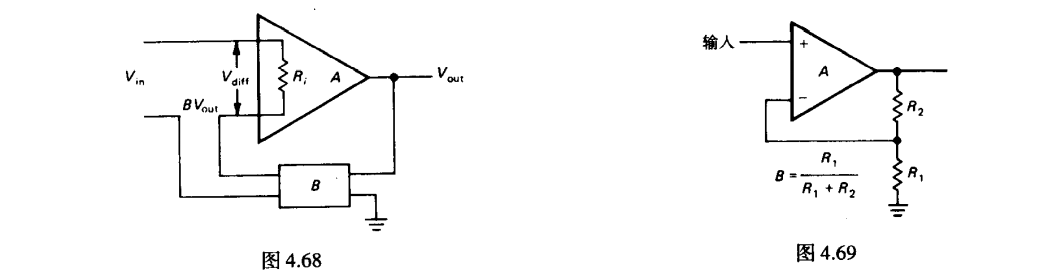
运放实际输入电压=1反馈深度闭环增益=A反馈深度运放实际输入电压=\frac{1}{反馈深度}\quad \\ 闭环增益=\frac{A}{反馈深度}运放实际输入电压=反馈深度1​闭环增益=反馈深度A​﻿

电压反馈(同相放大器)

电压反馈(同相放大器)

输入阻抗计算

Iin=Vin−BVoutRi=Vin/(1+AB)RiI_{in} = \frac{V_{in}-BV_{out}}{R_i}=\frac{V_{in}/(1+AB)}{R_i}Iin​=Ri​Vin​−BVout​​=Ri​Vin​/(1+AB)​﻿

可得Vout=Ri(1+AB)V_{out} = R_i (1+AB)Vout​=Ri​(1+AB)﻿

或者借助上面 各参数直观理解 的结论

设输入电压1 V

运放实际输入电压11+AB\frac{1}{1+AB}1+AB1​﻿

输入电流1(1+AB)Ri\frac{1}{(1+AB)R_i}(1+AB)Ri​1​﻿

输入阻抗1/1(1+AB)Ri=(1+AB)Ri1/\frac{1}{(1+AB)R_i} = (1+AB)R_i1/(1+AB)Ri​1​=(1+AB)Ri​﻿

输出阻抗

通用推导如下

我们知道若设V_{in}=1

则运放实际输入为1/反馈深度1/反馈深度1/反馈深度﻿

求输出阻抗,即输入短接,输出接电源

假设输出接的电压为A1+AB\frac{A}{1+AB}1+ABA​﻿,使得在求和点上反馈的量不变,而输入量变0

现在运放实际输入为1反馈深度−1\frac{1}{反馈深度}-1反馈深度1​−1﻿

运放的输出产生A(1−反馈深度反馈深度)A(\frac{1-反馈深度}{反馈深度})A(反馈深度1−反馈深度​)﻿的电压

Zo=A1+AB/A1+AB−A(1−反馈深度反馈深度)Ro−−−−−−−−−−−−−=Ro1+AB/(11+AB+AB1+AB)−−−−−−−−−−−−−=Ro1+ABZ_o = \frac{A}{1+AB} / \frac{\frac{A}{1+AB}-A(\frac{1-反馈深度}{反馈深度})}{R_o} 

\\-------------\\

=\frac{R_o}{1+AB} / (\frac{1}{1+AB} + \frac{AB}{1+AB})

\\-------------\\

=\frac{R_o}{1+AB}Zo​=1+ABA​/Ro​1+ABA​−A(反馈深度1−反馈深度​)​−−−−−−−−−−−−−=1+ABRo​​/(1+AB1​+1+ABAB​)−−−−−−−−−−−−−=1+ABRo​​﻿

对于同时电压电流反馈也具有Blackman Formula

Zo=Ro1+(AB)SC1+(AB)OCZ_o = R_o \frac{1+(AB)_{SC}}{1+(AB)_{OC}}Zo​=Ro​1+(AB)OC​1+(AB)SC​​﻿

(AB)SC(AB)_{SC}(AB)SC​﻿为输出短接到地的环路增益

(AB)OC(AB)_{OC}(AB)OC​﻿为无负载的环路增益

电流反馈(反相放大器)

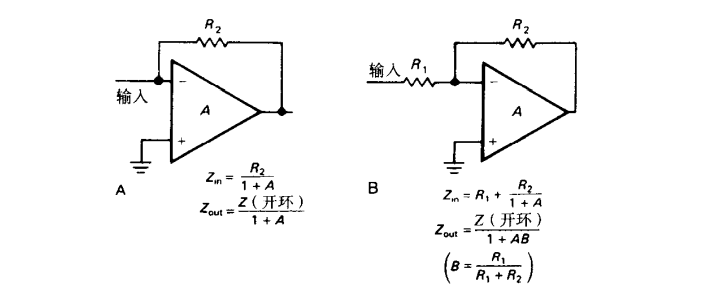
电流反馈(反相放大器)

非通用方法计算

假设R_2另一端接到地,则R_2两端压差为V_{in}

此处由于放大效应R_2两端压差为(A+1)V_{in} ,电流也为原来的A+1倍

故阻抗为原来的1A+1\frac{1}{A+1}A+11​﻿

则有输入阻抗为Ri∣∣R2A+1≈R2A+1R_i || \frac{R_2}{A+1} \approx  \frac{R_2}{A+1} Ri​∣∣A+1R2​​≈A+1R2​​﻿

反馈的通用分析方法(看成电阻+电流反馈)

将R1R_1R1​﻿和后面电路分离

只需要证明后一半电路的为电流反馈 且反馈深度为1/(1∣∣R2Ri(A+1))1/(1||\frac{R_2}{R_i(A+1)})1/(1∣∣Ri​(A+1)R2​​)﻿即可

设输入电流1 A

运放实际输入电流1反馈深度\frac{1}{反馈深度}反馈深度1​﻿

实际输入电压Ri反馈深度\frac{R_i}{反馈深度}反馈深度Ri​​﻿

输入阻抗Ri反馈深度/1=Ri反馈深度\frac{R_i}{反馈深度}/1 = \frac{R_i}{反馈深度}反馈深度Ri​​/1=反馈深度Ri​​﻿

若使得Ri反馈深度=Ri∣∣R2A+1\frac{R_i}{反馈深度} = R_i || \frac{R_2}{A+1}反馈深度Ri​​=Ri​∣∣A+1R2​​﻿

则有反馈深度为R2+Ri(1+A)R2=1+Ri(1+A)R2\frac{R_2+R_i(1+A)}{R_2}= 1+ \frac{R_i(1+A)}{R_2}R2​R2​+Ri​(1+A)​=1+R2​Ri​(1+A)​﻿(已知ZiZ_iZi​﻿逆向求反馈深度)

反馈深度计算

此处A为负数,为计算方便另A为整数,则增益为-A 

令RiR_iRi​﻿运放内阻 ZiZ_iZi​﻿为输入阻抗

在后面电路中为电流反馈,设Iin=1I_{in} = 1Iin​=1﻿ 则Vin=ZiV_{in} = Z_iVin​=Zi​﻿

则有I2=(1+A)Zi/R2I_2 = (1+A)Z_i/R_2I2​=(1+A)Zi​/R2​﻿

I1=1/反馈深度=Iin−I2=R2−(1+A)ZiR2I_1 = 1/反馈深度 = I_{in}-I_2 = \frac{R_2 - (1+A)Z_i}{R_2}I1​=1/反馈深度=Iin​−I2​=R2​R2​−(1+A)Zi​​﻿

反馈深度为  R2R2−(1+A)Zi\frac{R_2}{R_2 - (1+A)Z_i}R2​−(1+A)Zi​R2​​﻿

实际输入阻抗为RiR2−(1+A)ZiR2=ZiR_i\frac{R_2 - (1+A)Z_i}{R_2}=Z_iRi​R2​R2​−(1+A)Zi​​=Zi​﻿

Ri1+(Ri/R2)(1+A)=Zi\frac{R_i}{1+(R_i/R_2)(1+A)}= Z_i1+(Ri​/R2​)(1+A)Ri​​=Zi​﻿

RiR2R2+Ri(1+A)=R21+A∣∣Ri=Zi\frac{R_iR_2}{R_2+R_i(1+A)} = \frac{R_2}{1+A} || R_i = Z_iR2​+Ri​(1+A)Ri​R2​​=1+AR2​​∣∣Ri​=Zi​﻿

跟上面逆向推到相同

反馈深度快捷计算

结论 反馈深度=1+Ri(1+A)R2反馈深度=1+ \frac{R_i(1+A)}{R_2}反馈深度=1+R2​Ri​(1+A)​﻿

跟通用表达式比较 =1+AB= 1+AB=1+AB﻿

反馈深度 直接物理意义,将运放的直接输入作为1,可求得环路增益,1+环路增益1+环路增益1+环路增益﻿则为反馈深度

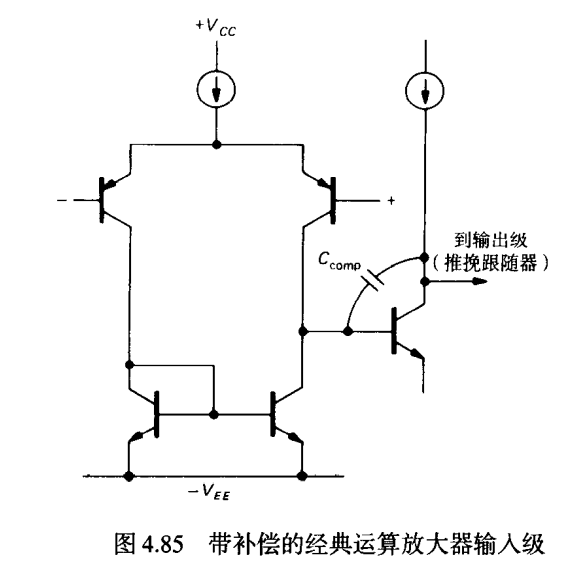
八.反馈放大器的频率补偿

为何需要频率补偿?

LM324原理图

增益下降原理分析

任何运放的增益在某些频率都会下降

由于有限的信号源内阻和运放各级电容形成了低通滤波器所导致的

假如移除补偿电容CcC_cCc​﻿则 输入级的高输出阻抗 和 结电容CieC_{ie}Cie​﻿ 下一级反馈电容CcbC_{cb}Ccb​﻿(密勒效应)构成了低通放大器-3db在100Hz-10K之间

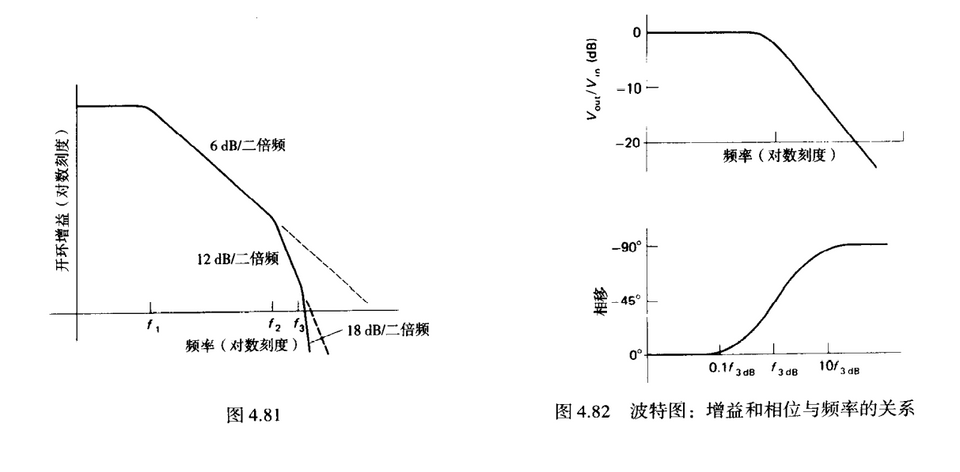
由于多级放大器,往往不止有一个滤波器,第二个滤波器和第一个同时作用于高频段造成了-12db/2倍频,第三个和前两个造成-18db/倍频 ... 依此类推

增益相位分析

增益-相位-频率分析图

解释1: 由于低通滤波器则有增益为-6db/2倍频下降

解释2: 

在高频段下电容负载在集电极的负载阻抗中占支配地位

则有增益G_v = g_mX_C 增益以1/f下降 即-6db/二倍频

相位也为90度的滞后

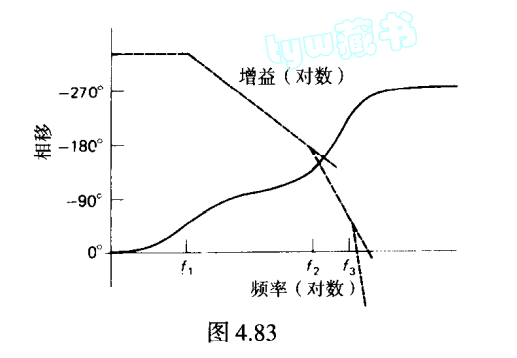
稳定性的判断

为了避免增益为1的时候相位差为180,防止负反馈变成正反馈,需要在高频段认为附加滚降

防止震荡的标准: 在闭环增益为1的频率上,相移<180,即跟随器形式

主要极点补偿

主要极点补偿

减少元器件差异

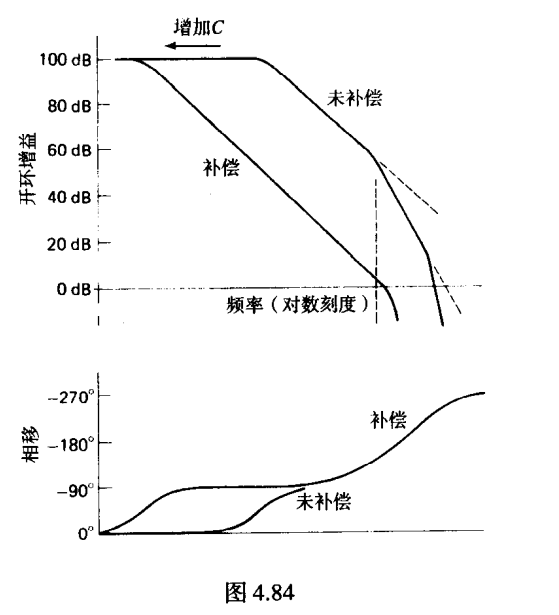
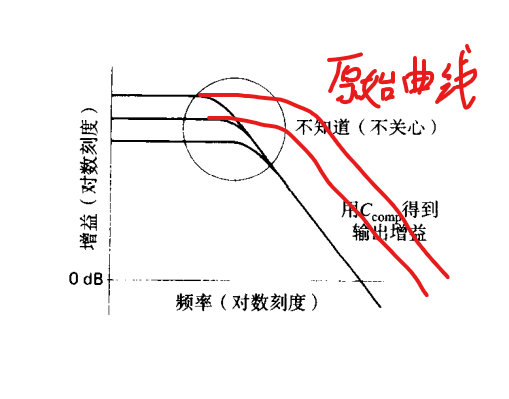
通过CcompC_{comp}Ccomp​﻿进行极点补偿

通过将主要极点提前,从而将滚降频率提前,避免不稳定性

通过在输入级的输出和放大级中接入电容,利用米勒效应

主动进行极点补偿还可以减少元器件的差异

极点-零点补偿

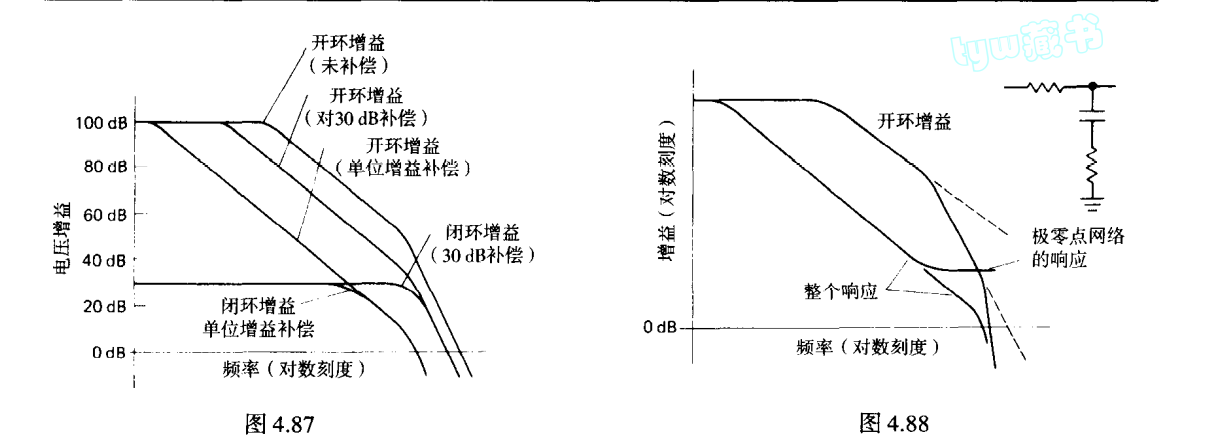
极点零点补偿

通过极点-零点补偿,抵消第二极点对曲线的影响,使得到第三极点处再滚降

反馈网络滚降的重要性

若将