Home
/
...
/
CSAPP
/
§2 Prepresrnting and Manipulating Information
Search
Try Notion
§2 Prepresrnting and Manipulating Information
Info Storge
信息在计算机内如何存取
程序将内存视为大数组, 每个字节都可以用地址表示
虚拟地址空间: 所有地址的集合
字节(Byte) : 8 Bit组成
Number System 进制
进制简介
有位模式 十进制表示法 16进制表示法(Hex Notation)
进制转换
bin2hex: 将位模式中4个位作为一个16进制
hex2bin: 进制转换小技巧: 记忆ACF(ACF Tips)
A: 10(Dec) 1010(Bin)
C: 12(Dec) 1100(Bin)
F: 15(Dec) 1111(Bin)
然后 B= A +1 D=C+1 E=F-1即可
2n2^n to Hex :
比如2112^{11}, 由于我们是4个二进制作为一个16进制
故有 11/4=3...211/4 = 3 ... 2 得到 211=(24)3∗(2)3=8∗163(Dec)=0x80002^{11} = (2^4)^3 * (2)^3 = 8 * 16^3 (Dec)= 0x8000
辗转相除法
我们不妨将数统一用十进制表示, 但是区别于位置计数法, 我们采用多项式展开形式表示
定义: 系数组合 anan−1..a1a_na_{n-1}..a_1 就是在 xx 进制下位置表示法
🤔其他进制在10进制下表现为: Num=a1∗x1+a2∗x2...Num = a_1*x^1 + a_2*x^2 ...
xx 代表进制基数如: dec为10 hex为16等等
ana_n 代表数 其不能超过进制基数, 否则本位减去基数, 下一位+1
进制转换: 本质上就是提取 ana_n 这个系数的具体值
我们有Num/x=anxn+...+a2x2...a1Num /x = a_n x^n+...+a_2x^2 ...a_1
通过余数, 我们便提取出了 a1a_1
我们只需要对剩下的部分反复使用辗转相除, 就可以提取出其他系数
Words
字长(Word):
一般决定虚拟地址空间的最大地址数
设字长 w bit , max Addr num: =2w−1w\ bit \text{ , max Addr num: } = 2^w-1
32-Bit and 64-Bit Program
一般64位字长机器都是兼容32位字长指令的
通过: gcc -m32 hello.c -o hello 或 gcc -m64 hello.c -o hello 可以指定32或64位指令集
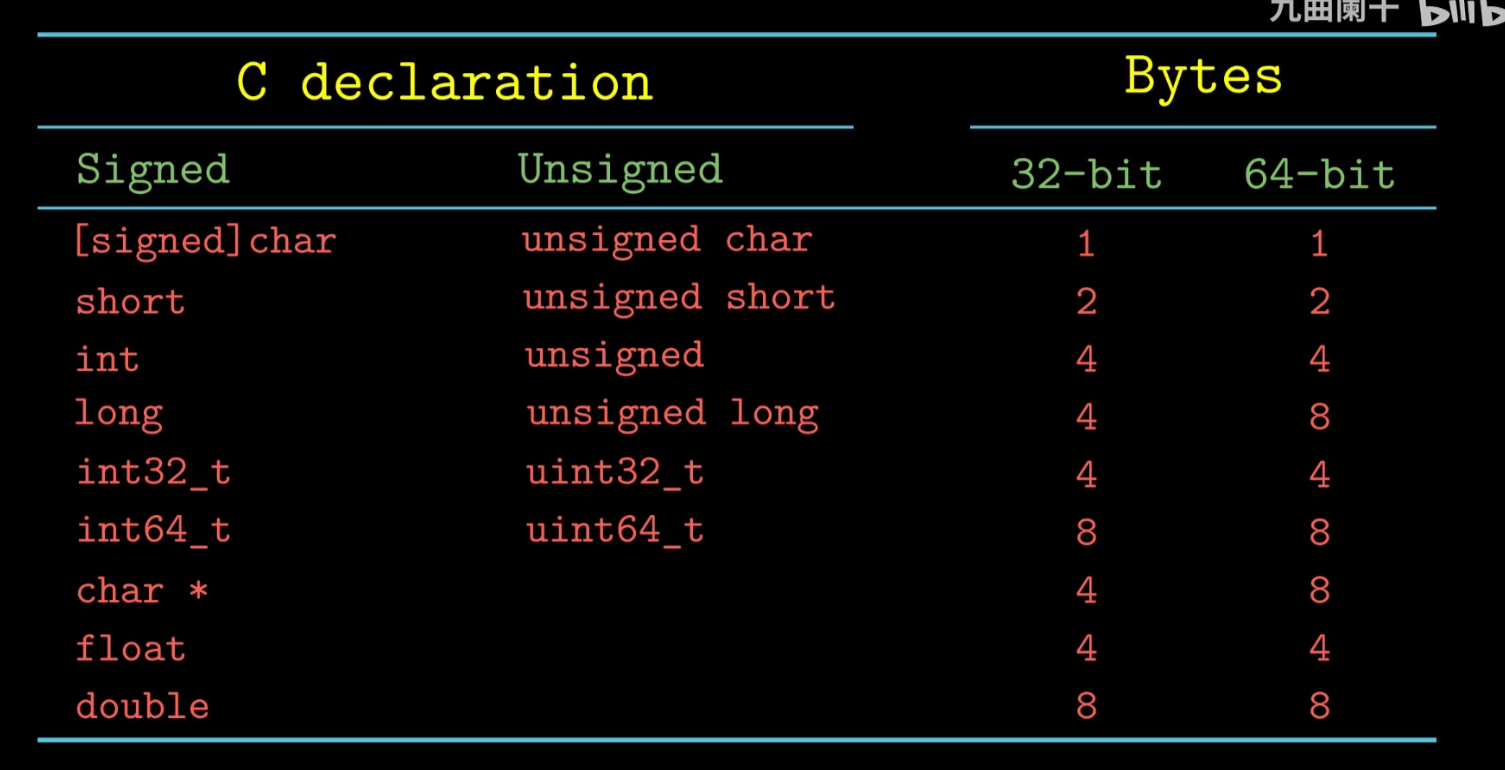
C语言中sizeof(Type) 表格
🖼️Sizeof(type) List in C
区别:
地址类型32位均为4Byte 64位均为8Byte (和机器字长相关)
long在32位中为4Byte 和 int 相同, 64位中long 为8Byte
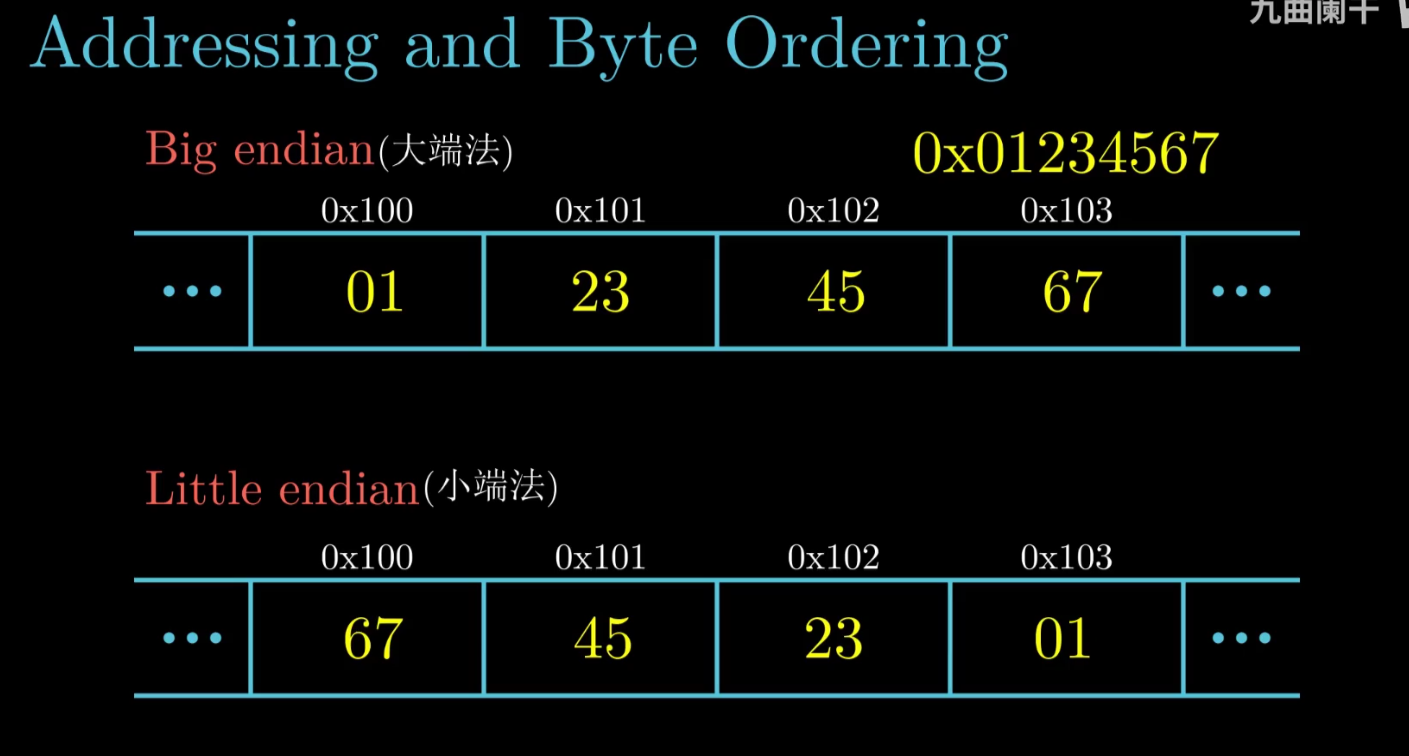
Byte Order
🖼️Byte Ordering
定义
Little endian: 位置计数法低位在低地址
Big endian: 位置计数法低位在低地址
注意: 涉及串口这类位发送的时候, 先发送Bit低位还是高位和Byte Order是两个概念
大小端例子
例子: IBM Sun兼容机使用大端法, Intel兼容机兼容小端法
也有大小端可变的处理器: 如ARM
但是IOS 和 Android都是只能运行在小端模式
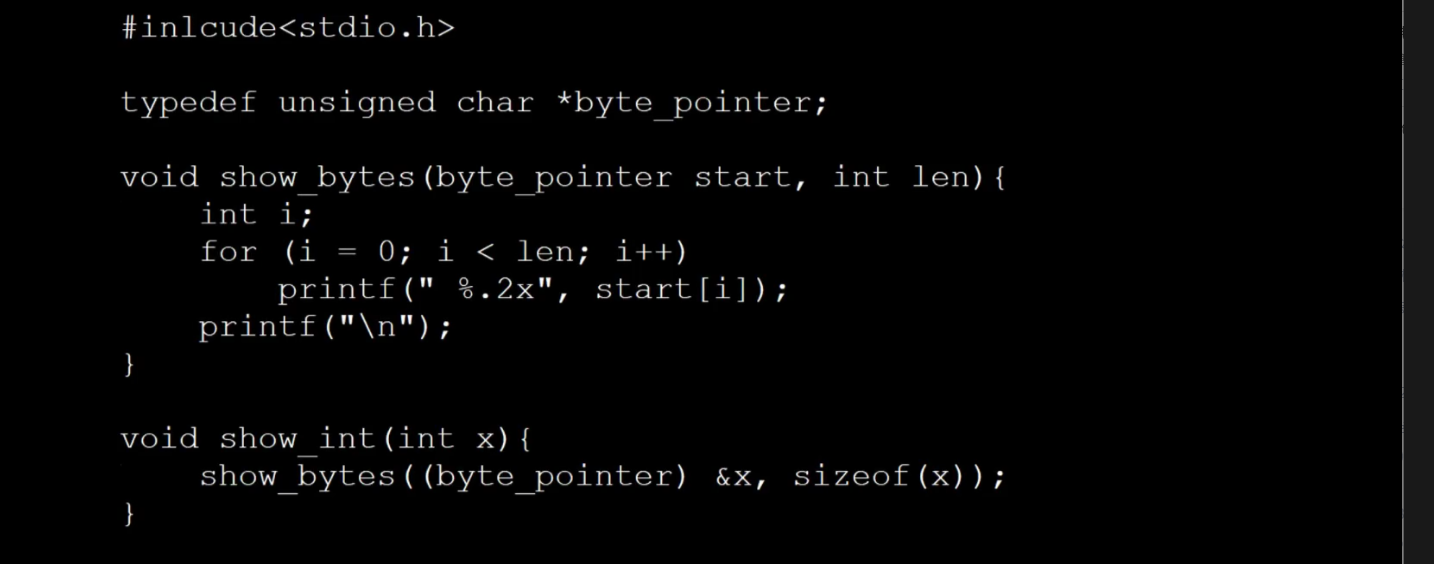
大小端Test Program
🖼️Test Program
整型浮点数编码引入
🖼️Coincidence in Float and Interger
当表示同一个数字时候, 整型浮点数有一段是完全匹配的, 这是为何?
C Style String
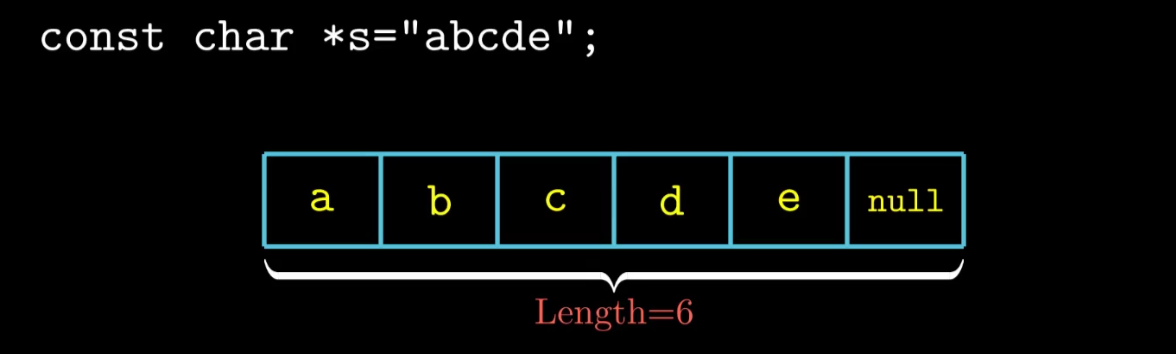
🖼️C Style String
结尾以null结尾(ASCLL码为0)
所以 sizeof(”12345”) == 6 需要考虑结束符
Boolean Algebra
逻辑运算: ~/NOT &/AND |/OR ^/XOR
C支持按位逻辑运算 和 普通逻辑运算
位运算用途: 掩码运算, 将特定位 Set Reset 和 反转
🤔Interger Represent
Some Basic Declare
其他进制 视作十进制Vetor的缩写 表示法
我们将表示和代表的数字分离, EveryThing Base on Dec
数的十进制表示我们也称 “数本身” , 所有数的表示我们都默认以十进制表示
数的其他进制表示我们视作向量 x⃗=[xw1,xw−2...x0]\vec{x} = [x_{w_1},x_{w-2}...x_0] 的一种缩写
我们接下来研究数的进制
传统的Dec Bin Hex表示法
上面的的Vetor表示法, 虽然足够清晰, 但是不符合数学的这项
这里我们根据CSAPP知识,重写一套体系 ,传统的的下标表示进制 是比较符合直觉的
不同进制表示符号 “本质”一致, 仅仅是表示不同的直觉
Hex Bin Dec 表示法相关规定
我们采用 AHex10Dec12Oct1010BinA_{ Hex }\quad 10_{ Dec } \quad 12_{Oct} \quad 1010_{Bin} 来区别同一数值不同进制下的表示法
或者我们也可以采用C Style 0x0A 10 012 表示不同进制(暂无二进制表示)
再或者我们可以采用Verilog Style 4'b1010 4'd35
其中 ' 前面代表数值在二进制表示法下所需的二进制空间
b h d 则代表了编码方式
计算机中我们扩展了几种的编码, 每位上同样
101016′u=10dec1010_{16'u} = 10_{dec}  表示16位Unsigned编码
101016′t=10dec1010_{16't} = 10_{dec} 表示16位Complement编码
1010w′t=10dec=101010_{w't} = 10_{dec} = 10 表示w位Complement编码
Unsigned and Two’s-Complement Represent
不同进制间的转换函数 numdec→numhexnum_{dec} \rightarrow num_{hex} , 所需的约定
当不标注下标的时候默认下标均为 decdec (十进制表示)
xix_i 表示数 xcodeingx_{codeing}  对应表示法下的第 ii 位
💡数学快换式: 基数为2的等比数列求和需要记忆 在求范围时候很有效
20+21…2i=2i+1−12^0 +2^1 \dots 2^i = 2^{i+1} -1
UtoD(xw’u)UtoD(x_{w’u}) 即Unsigned to Dec
📐U2D定义
xdec=U2D(xw′u)=xw−12w−1+xw−22w−2…x020=∑i=0w−1xi2i\begin{aligned} x_{dec}=U2D(x_{w'u}) &= x_{w-1}2^{w-1} +x_{w-2}2^{w-2} \dots x_{0}2^{0} \\ &=\sum\limits_{i=0}^{w-1} x_i2^i \end{aligned}
📐T2D值域(范围)
0≤U2D(xw′u)≤2w−1+2w−2+⋯+20=2w−1⇕0≤U2D(xw′u)<2w\begin{aligned} 0 \leq U2D(x_{w'u}) \leq & 2^{w-1}+2^{w-2} + \dots + 2^0 \\ =&2^w-1 \end{aligned} \\ \Updownarrow \\ 0 \leq U2D(x_{w'u}) < 2^w
TtoD(xw’u)TtoD(x_{w’u}) 即Two’s-complementto Dec
📐T2D定义
xdec=T2D(xw′t)=−xw−12w−1+xw−22w−2…x020=∑i=0w−1xi2i\begin{aligned} x_{dec}=T2D(x_{w't}) &= -x_{w-1}2^{w-1} +x_{w-2}2^{w-2} \dots x_{0}2^{0} \\ &=\sum\limits_{i=0}^{w-1} x_i2^i \end{aligned}
📐T2D值域(范围)
−2w−1≤T2D(xw′t)≤2w−2+2w−3+⋯+20=2w−1−1⇕−2w−1≤T2D(xw′t)<2w−1\begin{aligned} -2^{w-1} \leq T2D(x_{w't}) \leq & 2^{w-2}+2^{w-3} + \dots + 2^0 \\ =&2^{w-1}-1 \end{aligned} \\ \Updownarrow \\ -2^{w-1} \leq T2D(x_{w't}) < 2^{w-1}
D
Floating Point
浮点数的组成
浮点数的数值组成: V=(−1)s∙M∙2EV = (-1)^s \bullet M \bullet 2^E 三个部分 s M E
二进制编码组成: s exp frac
其中: s→s exp→E frac→M 这三个部分的组成
二进制编码和数值的对于关系
Float Type General
Normalized ( exp(dec)≠0∣∣exp(dec)≠255exp_{(dec)} \neq 0 ||exp_{(dec)} \neq 255 )
Denormailzed ( exp(dec)=0exp_{(dec)} = 0 )
Infinity ( exp(dec)=255exp_{(dec)} = 255 )
Normalized ( exp(dec)≠0∣∣exp(dec)≠255exp_{(dec)} \neq 0 ||exp_{(dec)} \neq 255 )