信号与系统

信号与系统

一.导论

消息: 通讯系统中,语言 文字 图像 数据称为消息

信号: 消息的表达形式和载体 消息是信号的内容

描述方法: 一个或多个函数的叠加

分类

确定性信号: 已知t 知道函数值

随机信号: 有专有描述方法一般分析其统计特性

连续信号: 任意时刻均有定义

抽样: 使得自变量离散 幅值依旧连续

量化: 幅值也离散

最后称数字信号

离散信号: ...

系统: 具有若干相互作用 互相依赖的稳定功能整体

对输入信号(激励)加工处理为输出

信号理论 系统理论

信号分析 处理 传输

系统分析 给定系统 研究输入输出

系统综合 按要求设计所需系统

系统示例:

通讯系统: 用电信号传递

信号处理

滤波

模式识别

二.连续信号

常见连续信号

指数信号

微分积分后依旧指数

一般为单边

时间常数越大,变化越慢(常用单边)

正弦信号

角频率

初相位

可转化为时移

连续信号运算

相加相乘

微分积分

奇异信号: 函数本身或其导数积分有不连续点(跳变点)的函数

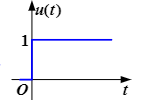
单位斜边信号: R(t)=0 t<0 or t t≥0R(t)=0\  t<0 \ or\  t\  t≥0R(t)=0 t<0 or t t≥0﻿

单位阶跃信号: u(t)=0 t<0 or1 ≥0u(t)=0 \ t<0 \ or 1 \ ≥0u(t)=0 t<0 or1 ≥0﻿

函数图像-单位阶跃

表示门(Gate)函数

表示符号(Gate)函数

单位冲击信号

定义1: 脉冲信号取极限 p(t)=1τ[u(t+τ2)−u(t−τ2)]τ→0p(t)=\frac{1}{\tau}[u(t+\frac{\tau}{2}) - u(t-\frac{\tau}{2})] \quad \tau \rightarrow 0p(t)=τ1​[u(t+2τ​)−u(t−2τ​)]τ→0﻿

定义2: Dirac狄拉克函数 ∫−∞+∞δ(t)dt=1且δ(t)=0t≠0\int_{-\infty }^{+\infty } \delta (t) dt= 1 且 \delta (t) =0 \quad t≠ 0∫−∞+∞​δ(t)dt=1且δ(t)=0t=0﻿

定义3: 广义函数定义(基于分配函数理论)
 ∫−∞+∞δ(t)f(t)dt=f(0) \int_{-\infty }^{+\infty } \delta (t) f(t)dt= f(0) \quad ∫−∞+∞​δ(t)f(t)dt=f(0)﻿

且f(t)需所有阶数连续 且f(t)≠0且f(t) 需所有阶数连续\ 且f(t) \neq 0且f(t)需所有阶数连续 且f(t)=0﻿ 

性质: 

其积分为1 无界函数

抽样性: 

若f(t)f(t)f(t)﻿在t=0t=0t=0﻿时连续且处处有界
则 ∫−∞+∞δ(t)f(t)dt=f(0)\int_{-\infty }^{+\infty } \delta (t) f(t)dt= f(0) ∫−∞+∞​δ(t)f(t)dt=f(0)﻿
或表示成 δ(t)f(t)=δ(t)f(0)\delta (t) f(t) = \delta (t) f(0)δ(t)f(t)=δ(t)f(0)﻿

奇偶性

证明1: 由定义1(脉冲取极限)可直接得偶函数

证明2:

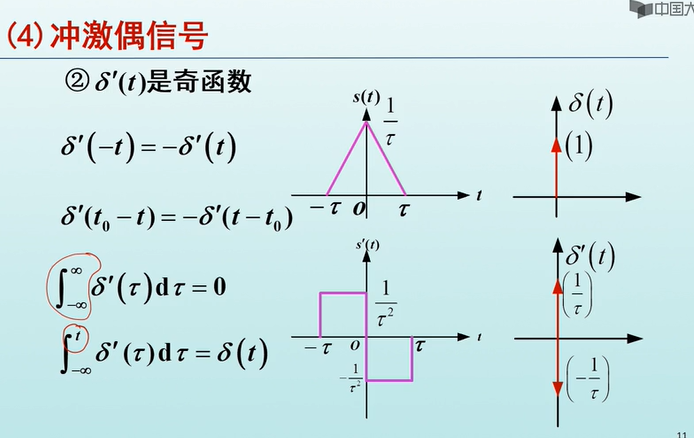
已知: \int_{-\infty }^{+\infty } \delta (t) f(t)dt= f(0)\\ 即证: \int_{-\infty }^{+\infty } \delta (-t) f(t)dt= f(0)

冲击偶函数: 一对正负 大小为无穷大

为单位冲击函数求导

积分后抽样求导特点

证明过程

函数本身为奇函数

证明过程

乘法后特性

证明

注意:选择可行

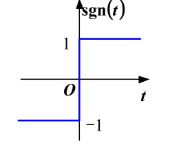
阶跃信号

自变量变换

平移

反转: 过去未来对调

尺度变换

信号分解

直流交流分解

直流分量f_D(direct current component): 信号得平均值

交流分量f_A(alternating current component): 信号减去平均值后的(积分为0)

功率计算

对信号平方再积分求平均

非平方项由于交流积分为0,约去

只剩交流项 直流项各自的平方(积分正交)

频率正交推导(功率平方可叠加)

功率的

奇偶分解

fef_efe​﻿(even component)

fof_ofo​﻿(odd component)

信号计算

推导

功率计算

同样先平方,在积分,最后平均

依旧为积分正交(平方可叠加)

推导

虚实分解

信号计算

共轭方法

三.离散信号

离散信号的表示: 先定义连续x(t)x(t)x(t)﻿函数,然后令ttt﻿表示特定序列nTsnT_snTs​﻿ 表示为x(n)x(n)x(n)﻿

常见信号

单双边信号分类: n≥0 单边信号 n∈\in∈﻿N 为双边 n∈\in∈﻿[区间] 为有限长序列

单位样值信号(kronecker信号)

符号同Dirac信号同为δ\deltaδ﻿

δ(n)=1,n≠0 or 1,n=0\delta(n)= 1,n≠0 \ or \ 1,n=0δ(n)=1,n=0 or 1,n=0﻿

抽样性

时移性

可以用样值信号表示任意信号

x(n)=∑m=−∞∞x(m)δ(n−m)x(n)=\displaystyle\sum_{m=-\infty}^{\infty}x(m)\delta(n-m)x(n)=m=−∞∑∞​x(m)δ(n−m)﻿x(n)=\displaystyle\sum_{m=-\infty}^{\infty}x(m)\delta(n-m)

x(m)x(m) x(m)﻿表示权重序列 δ(n−m)\delta(n-m)δ(n−m)﻿ 表示位置

单位阶跃信号

u(n)=1,n≥0 or 1,n=0u(n)= 1,n≥0 \ or \ 1,n=0u(n)=1,n≥0 or 1,n=0﻿

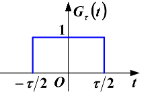
也可用单位样值信号表示u(n)=δ(n)+δ(n−1)+δ(n−2)... u(n)=\delta(n) +  \delta(n-1) + \delta(n-2) ...u(n)=δ(n)+δ(n−1)+δ(n−2)...﻿

矩形序列

RN(n)=1,N−1>n≥0 or 0,其他R_N(n)= 1,N-1>n≥0 \ or \ 0,其他RN​(n)=1,N−1>n≥0 or 0,其他﻿

RN(n)=u(n)−u(n−N)R_N(n)=u(n)-u(n-N)RN​(n)=u(n)−u(n−N)﻿

斜边序列

单边指数序列

正弦序列

 xa(t)=sin(2πf0t)=sin(Ω0t)x_a(t)= sin(2\pi f_0t)=sin(\Omega_0 t) xa​(t)=sin(2πf0​t)=sin(Ω0​t)﻿

抽样间隔TsT_sTs​﻿ 抽样率fsf_sfs​﻿  xa(Tsn)=sin(Ω0Tsn)=sin(ω0n)x_a(T_sn)=sin(\Omega_0 T_s n) =sin(\omega_0 n)xa​(Ts​n)=sin(Ω0​Ts​n)=sin(ω0​n)﻿

ω0\omega_0 ω0​﻿为数字角频率 Ω0\Omega_0 Ω0​﻿为模拟角频率

正弦序列若要是周期序列则有x(n+N)=x(n)x(n+N)=x(n)x(n+N)=x(n)﻿ 

若有 w0N=2π∗nw_0N= 2\pi *nw0​N=2π∗n﻿ 或者2π/w02\pi/w_0 2π/w0​﻿为有理数

复指数序列

运算

相加: 序列不够长补0运算

移位

倒置

差分

前向差分: Δx(n)=x(n+1)−x(n)\Delta x(n) = x(n+1) - x(n)Δx(n)=x(n+1)−x(n)﻿

后向差分: ∇x(n)=x(n)−x(n−1) \nabla x(n) = x(n) - x(n-1)∇x(n)=x(n)−x(n−1)﻿

累加

重排

抽取(decimation): x(n)→x(Nn)x(n)→x(Nn) x(n)→x(Nn)﻿ 只保留整数

内插: x(n)→x(n/2) 可先插0值

能量

先平方,再求和

E=∑n=−∞∞∣x(n)∣2E=\displaystyle\sum_{n=-\infty}^{\infty} |x(n)|^2E=n=−∞∑∞​∣x(n)∣2﻿

平均功率

周期序列下 P=1N∑n=0N−1∣x(n)∣2P=\frac{1}{N}\displaystyle\sum_{n=0}^{N-1} |x(n)|^2P=N1​n=0∑N−1​∣x(n)∣2﻿

非周期下P=lim12K+1∑n=−KK∣x(n)∣2P=lim \frac{1}{2K+1}\displaystyle\sum_{n=-K}^{K} |x(n)|^2P=lim2K+11​n=−K∑K​∣x(n)∣2﻿

三.系统

系统分类

离散 连续: 输入输出是否都是离散或连续

及时 动态: 是否和之前状态有关

集中参数: 仅关于时间t

可逆系统: 不同激励→不同响应(一一对应)

线性系统: 线性组合的输入经过系统等于输入单独的输入的的线性组合

均匀性: ...

叠加性: ...

时不变系统: 零初始条件下 输入信号与输出信号与时间起点无关

特征

电路的元件不变化

方程系数不改变

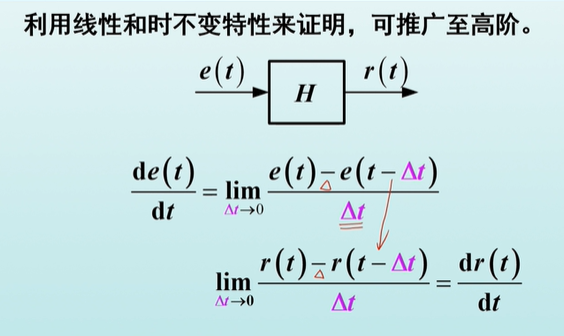
线性时不变: LTIS liner and time invariant system

微分性质: 将输入微分(n阶)送进系统,则输出也相应为源输出的(n阶)微分

微分系统证明

因果系统: 仅当输入信号激励系统时候才产生输出

判断: 输出是否超前输入

因果信号: 单边信号 即t<0时e(t)=0即 t<0时e(t)=0即t<0时e(t)=0﻿

稳定系统: 对任何有界输入,都产生有界输出 boundary input boundary output BIBO

线性时不变系统分析方法

系统模型描述法

状态变量描述法: 可以描述内部变量的关系 多个一阶微分方程

输入输出描述法: 着眼输入输出关系,不考虑内部 1元n阶微分方程

求解方法

时域分析

经典的微分(连续) 差分(离散)方程

卷积

变换域分析

傅里叶变换FT

拉普拉斯变换LT

ζ\zetaζ﻿变换ZT

离散傅里叶DFFT

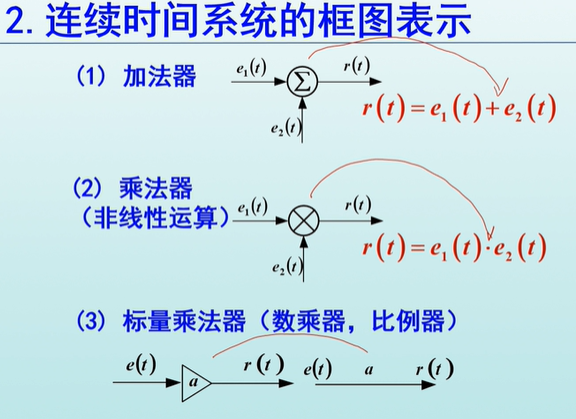
框图表示

加分器

乘法器(非线性)

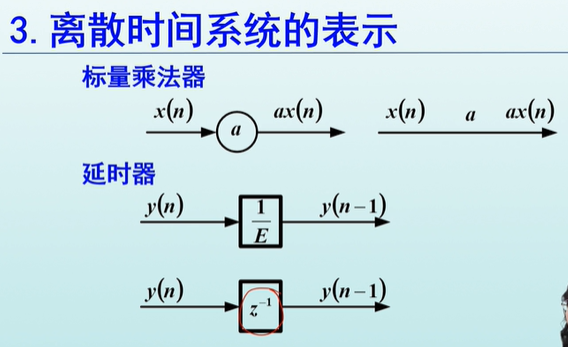
比例器

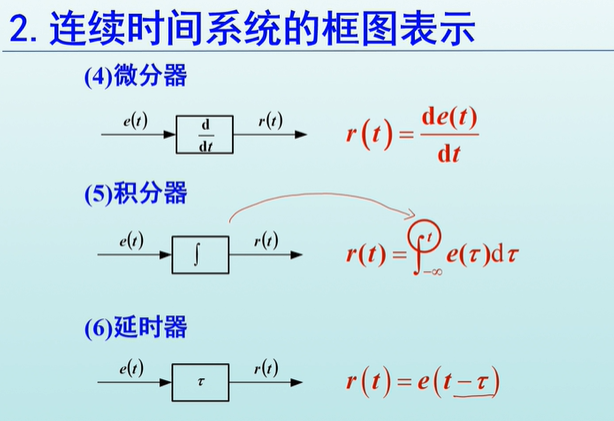
微分器

积分器

延迟器

差分器(离散)

框图图示