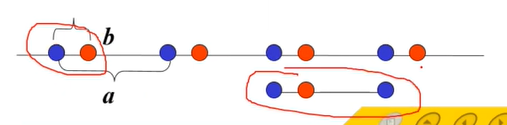
一.一维情况
一维单原子链
特征:
一维双原子链
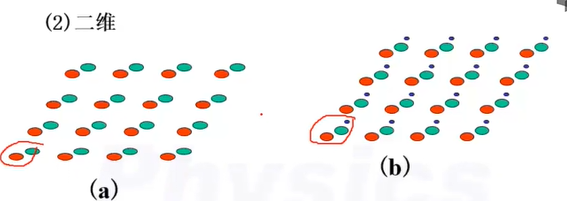
二.二维情况
二维的情况
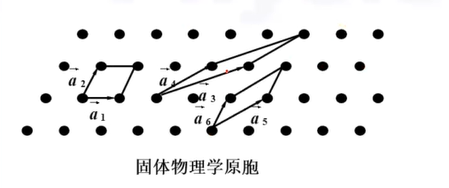
选择方法不唯一
但是面积都是一样的
三.三维情况
立方晶系
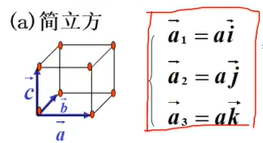
简立方
晶胞包含的格点计算方式
每个晶胞有8个格点
每个格点属于该晶胞的为1/8(每个格点都被8个晶胞共同拥有)
固体物理学原胞的体积计算方式
由于晶胞和原胞在简立方中一致
故:
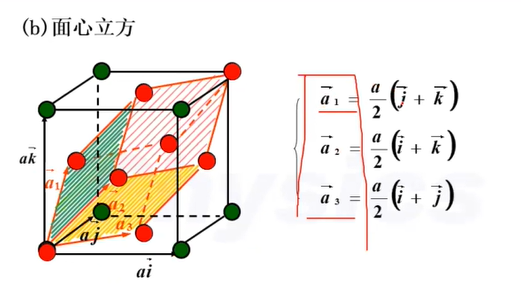
面心立方
老师注: 需要记忆
面心立方格点计算
8个顶点8个格点,每个格点被8个晶胞所有故为
6个面6个格点,每个格点被2个晶胞所有 故为
综上:
原胞体积计算
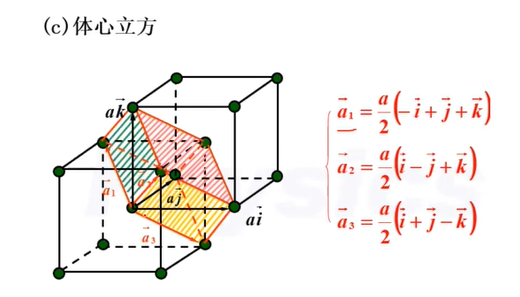
体心立方
晶胞包含的格点计算
8个顶点8个格点,每个格点被8个晶胞所有故为
体内1个格点,没有和其他共有
综上为
原胞体积计算
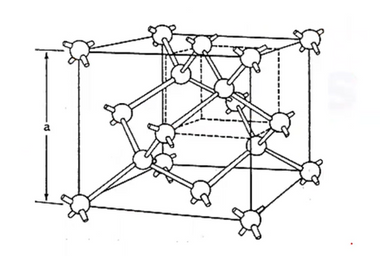
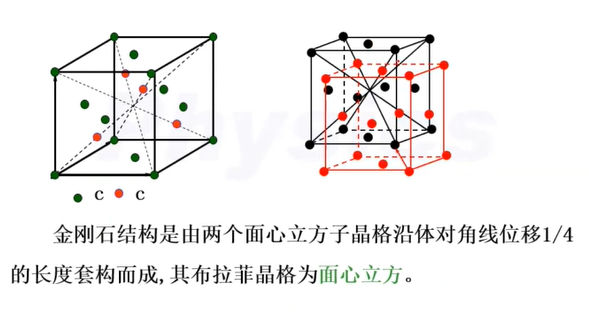
四.复式格
复式格
晶胞选取方法
格点计算方法