一.简介
都是递归调用的的算法,为何选择Quick-Sort而非Merge-Sort:
而非在最坏情况下时间复杂度为但是平均性能非常好为且常数因子非常小
可以进行原址排序
二.代码解析
Quick-Sort(A,p,r)
{
if(p<r)
{
init q = partion(A,p,r)
Quick-Sort(A,p,q-1)
Quick-Sort(A,q+1.r)
}
}
partion(A,p,r)
{
init key = A[r]
init key_index = p
for(i = p to r-1)
{
if A[i]<A[r]
{
exchange A[key_index] with A[i]
key_index ++
}
else{ continue }
}
exchange A[key_index] with A[r]
return key_index
}
Copy
C
Quick-Sort主代码解析
分解: 将A[p,r]划分成两个子数组A1[p,q-1] A2[q+1,r]使得A1中每个元素都小于A2
解决: 递归调用快速排序,假设调用后A1 A2已经有序
合并: 由于原址排序,故天然不需要合并
Partion代码分析
选定Key(Pivot轴): 此处任意选择都可,此处以A.end为轴
循环表达式证明满足A1中元素小于A2
初始化: key_index = p , 令A[p,key_index-1]为A1 , A[key_index,r]为A2
初始化的时候有A1[p,p-1]= 显然成立
保持: 当A[p,i]中的A1 A2符合循环条件(A1中元素小于A2中元素时候),将A变为A[p,i+1]
通过比较A[i+1]和pivot的大小,决定将A[i+1]放置到A1中还是A2中
并改变key_index即A1 A2的区分下标
结束: 结束的时候A[p,i]变为A[p,r-1]且有A1[p,key_index]中元素始终小于A2[key_index,r]中元素
收尾工作: exchange A[key_index] with A[r]
则有A2整体后移一位即A2[key_index,p-1] 变为 A2[key_index+1,p] 完成Partion
三.时间复杂度分析
非随机化下复杂度的直观分析
最坏情况分析
当产生的子问题包含n-1个元素和0个元素时候
最好情况分析
当产生的子问题包含个元素和个元素时候
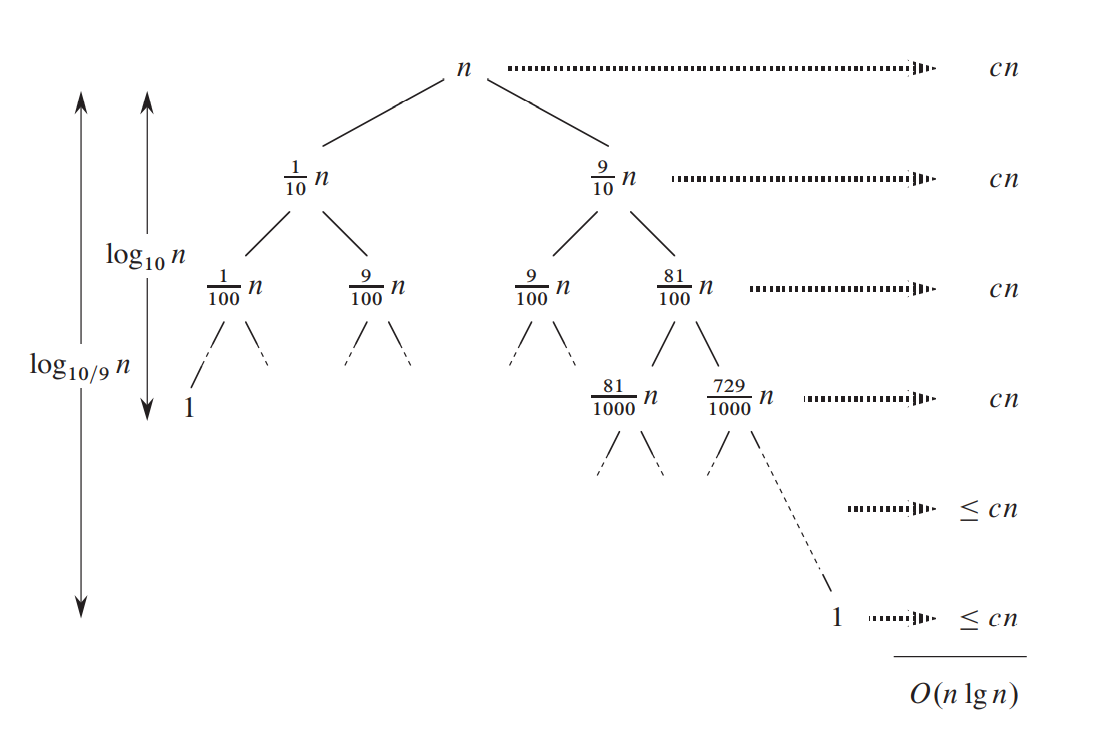
不平衡划分时候
假设每次都采取了1:9的划分比例
则可以列出如上时间树
可以观察到每一行的时间代价依旧为cn
则有
平均情况分析(粗略)
随机化Randomize-QuickSort期望
由于执行最多的语句为比较操作,我们以比较操作作为衡量该算法复杂度的操作
具体到本次例子,T(n)的关键在于Partion的调用,每次调用Partion会有的时间花费,而h的大小取决于for循环的次数,for的次数与( Pivot的选择 与 传入的数组大小A)有关,for循环的意义则是比较
Pivot的选择 与 传入的数组大小A)有关,for循环的意义则是比较
分析规则
由于Partion调用了n次(每个元素都需要当作Key(Pivot)被传入函数中,且进仅被调用一次)
其中X为比较次数
定义随机变量指示器为当, 进行比较时为1,其中为A的正确排序下的元素标号
则有 即为与X的基本计数单位
求期望比较的次数
关键在于 等于Z[i..j]中i被第一个选为Pivot的概率+ j被第一个选为Pivot的概率
引入随机性: 由于Z[i..j]中元素每个机会均等无特殊性,且互斥(只能有一个Pivot) 故有
综上可解