二.电容电感

二.电容电感

电容

在无分数表达式下Q=CVQ=CVQ=CV﻿ or I=Cdv/dtI=Cdv/dtI=Cdv/dt﻿ 下C位于V边,故为导性

RC电路参数确定

表达式V=B+Ae−t/τV=B+Ae^{-t/\tau}V=B+Ae−t/τ﻿仅有两个系数要确定 指数系数A 偏移系数B

指数系数 仅和V0 VtV_0\  V_tV0​ Vt​﻿的相对值有关 故为V0−VtV_0 - V_tV0​−Vt​﻿

偏移系数 可以视作t→∞t→\inftyt→∞﻿时候的值等于VtV_tVt​﻿

VVV﻿表示电容两端电压

虽然V0 VtV_0 \ V_tV0​ Vt​﻿是以RC为整体的二端元件分析的,但结论却是里面的内部结构

5τ5\tau5τ﻿准则: 5τ5\tau5τ﻿后当前值同极限值差距不超过1%

戴维南定理扩展

三极限法

积分电路

原理: 考虑如下图形

当位于起始阶段时候,近似直线(类似于积分)

故若想获得积分器.可将τ\tauτ﻿增大,来获取更大的直线近似区间

原理2;

I=CdVdt=Vin−VRI=C\frac{dV}{dt}=\frac{V_{in}-V}{R}I=CdtdV​=RVin​−V​﻿

得RCdVdt=Vin−VRC\frac{dV}{dt}=V_{in}-VRCdtdV​=Vin​−V﻿

当RC较大时候,有RCdVdt≈VinRC\frac{dV}{dt}\approx V_{in}RCdtdV​≈Vin​﻿

当RC比较大时候VinV_{in}Vin​﻿变化比较慢故有VinV_{in}Vin​﻿近似0,可忽略

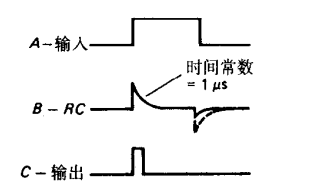
微分电路

原理分析: 基本同上...

注意:

由于积分电路为取R两端电压作为输出
在0状态响应下,恰好为Vin−VV_{in}-VVin​−V﻿,和上图图像上"互补"
若要达成比较好的微分效果,则RC应该比较小(??)

不要使得R过小,因为换路时候C两端电压不变,则电路中被视作只有R,瞬时功耗大

应用

前后沿检测图示

可以检测信号的前沿后沿: 微分后形成正负尖脉冲

容性耦合分析

容性耦合分析图

上图分析: 耦合进一个方波,由于微分器,变为一个个脉冲

改善:

信号通路上缺少阻性负载(??)

减小源电阻

其他

下图分析: 原方波信号,由于在电路某点端口,导致形成小电容

电感

变压器: 变压器能转换电压的本质在于共享了磁场,若有一个电容器C1C_1C1​﻿,可以将存储的电量直接转移导C2C_2C2​﻿电容器,若C1C_1C1​﻿,C2C_2C2​﻿不同且有Q=C1V1=C2V2Q=C_1V_1=C_2V_2Q=C1​V1​=C2​V2​﻿,则就实现了变压?(变容变压器)