Home
/
...
/
The Art of Electronics
/
五.三极管
Search
Try Notion
五.三极管
一.三极管的理论基础
基本简易模型
饱和-放大电位分析法(集电极不能大于Base)
Base-Emitter类似二极管
IC=βIBI_C=\beta I_B
IC IB VCEI_C\ I_B\ V_CE均存在最大数
🤔注意区分和饱和得区别 ...
其他非理想影响
Early效应(基区宽度调制效应)
第一表达式: 大信号模型中,加入厄利电压修正系数: IC=ISeVBEVT(1+VCEVA)I_{{\mathrm {C}}}=I_{{\mathrm {S}}}e^{{{\frac {V_{{\mathrm {BE}}}}{V_{{\mathrm {T}}}}}}}\left(1+{\frac {V_{{\mathrm {CE}}}}{V_{{\mathrm {A}}}}}\right)
VAV_{{\mathrm {A}}}是厄利电压（一般为15 V－150 V，对于小型设备会更小）
或者修正β\beta参数 βF=βF0(1+VCEVA)\beta_{{\mathrm {F}}}=\beta _{{\mathrm {F0}}}\left(1+{\frac {V{{\mathrm {CE}}}}{V{{\mathrm {A}}}}}\right)
第二表达式: 若使得ICI_C固定,则VCEV_{CE}为输入,VBEV_{BE}为输出则有 ΔVBE=−αΔVCEα≈10−4\Delta V_{BE} = -\alpha \Delta V_{CE} \quad \alpha \approx 10^{-4}
温度依赖:
Base级偏置电压很难加,数据可测 得固定ICI_C下VBE减小2.1mv/°CV_{BE}减小2.1mv/°C
β\beta 同样有温度依赖性(往往影响不大,通过RER_E电阻解决)
rerπr_e r_\pi(小信号才需要分析)非线性
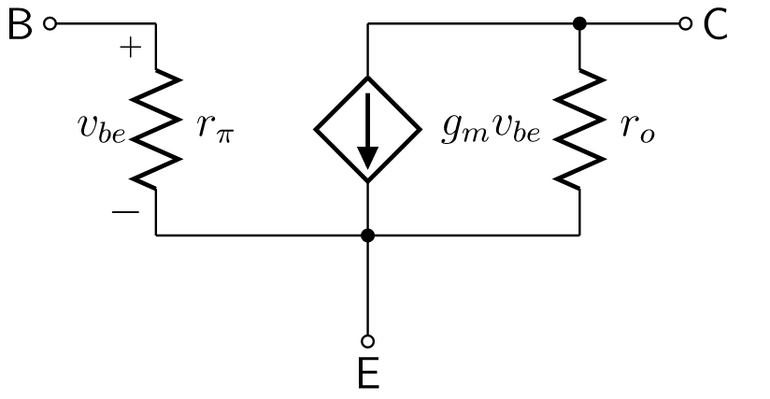
小信号模型
rer_e电阻模型
注意区别于rπr_\pi,虽然表达式相同,但似乎仅用于共射电路的分析
混合π\pi模型
🖼️Hybrid-π\pi模型图像
🤔形象理解
跨导为 gm=∂iC∂vBE=IC/VTg_m = \frac{\partial i_C}{\partial v_{BE}}=I_C/V_T
由于iC=β0iBi_C = \beta_0 i_B 导性变小了 故gπ=1rπ=gmβ0g_{\pi} = \frac{1}{r_{\pi}} = \frac{g_m}{\beta_0} 
CE回路的电阻(Early效应)go=1ro=∂iC∂vBE=IC/VAg_o = \frac{1}{r_o}=\frac{\partial i_C}{\partial v_{BE}}=I_C/V_A
🤔两种模型统一
本质上是一种模型,也可互相转换
🤔三种放大器电路拓扑系统分析
直流模型下
直流偏置选择问题: 交直流阻抗不一致的利用 有源偏置的使用
三极管
交流模型下
ri ro Avr_i\ r_o\ A_v  的系统分析
晶体管开关电路
确保VB>VEV_B>V_E
权衡: 本质上是个是否有足够电流和功率损耗得问题
灯冷电阻很低,V_CE初始比较大 \beta 在饱和区域很低
但进入饱和态需要大得I_B电流,损耗上升
可以适当得进入深度饱和状态,以降低功耗当β<10\beta < 10 时候则大致为饱和状态
🤔三极管的期望ICI_C
将处于放大态时候I_C=\beta I_B称为期望I_C
假设目前在放大态: 当IBI_B增大时候,ICI_C增大(放大态)CE回路上电阻所占据的的电压也增大,"压迫"VCEV_{CE}减小.当VCE=VCE(sat)=0.3VV_{CE}=V_{CE(sat)}=0.3V的时候
I_C
二.射级跟随/射级放大电路
射级跟随电路
负载含电压源问题(不能输出灌电流)
🖼️图示灌电流
基本原理:三极管只能提供拉电流
对三极管而言,E点只能流出电流
如果RLR_L为无源(此处地也为电源)则一切无事
但是若RLR_L为有源,当Vout<5VV_out < 5V时,以输出节点做分析,电流会倒灌进入三极管
直流偏置的选择
推挽放大
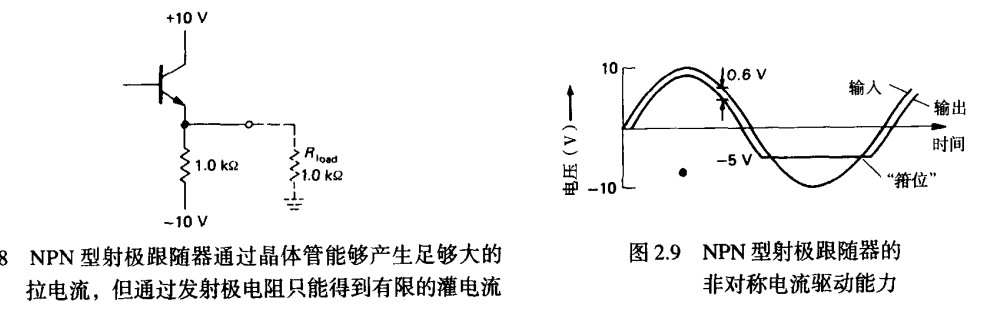
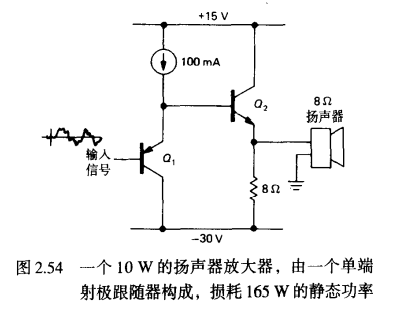
A类非推挽跟随器(功率放大)
🖼️A类跟随器
缺点: 以NPN为例子,由于NPN本身不能灌电流,则需要一个很小的接地电阻(跟R_L一致),来提供跟随器有可能遇到的灌电流,导致静态功耗十分大
B类推挽:
🖼️直接推挽
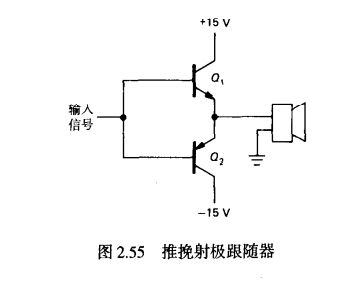
🖼️二极管对称偏置推挽
B类定义: 仅仅只有一个三极管极管处于导通状态
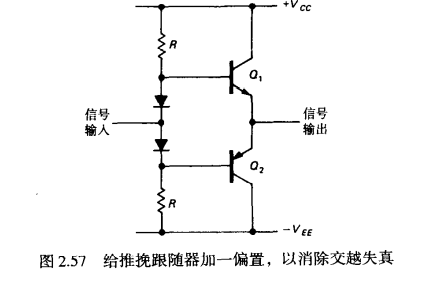
直接推挽有交越失真的风险,有偏置的话修成了了该问题
但是二者都存在热失控
AB类推挽
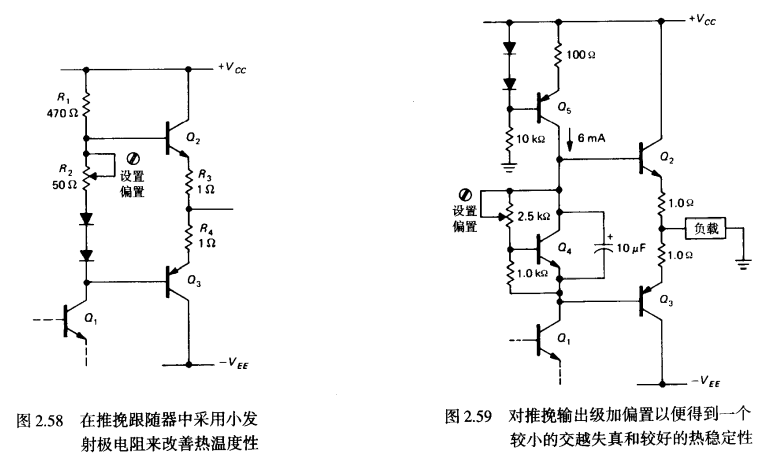
🖼️AB类推挽
反馈推挽放大: 修正了热失控 缺点: 有静态电流,静态功耗
共射放放大器
接电Base跟随缺陷
非线性: 接地后,Base电流完全依赖于rπr_\pi 电阻非恒定值,ICI_C随输入的变换而变化,故输出也随输入变化而变化
温度依赖: Base级偏置电压很难加,数据可测 得固定ICI_C下VBE减小2.1mv/°CV_{BE}减小2.1mv/°C
注意: 变换的是ICI_C减小得意思为,为了使ICI_C保持在同一水平，VBEV_{BE}必须是(外部!)减少 🔗来源 🔗理论推导
改进措施
射级电阻改进: 接入RER_E 使得输入阻抗取决于RER_E而非rπr_\pi
并联电容改进: RER_E并联电容,使得交流阻抗减小,提升增益
匹配偏置: 加入第二个晶体管可以用于改进温度偏移
直流反馈
...
可加入旁路电容消去交流反馈
0温漂补偿电路 ...
单位增益反相器
可作为移相器
三.电源类电路
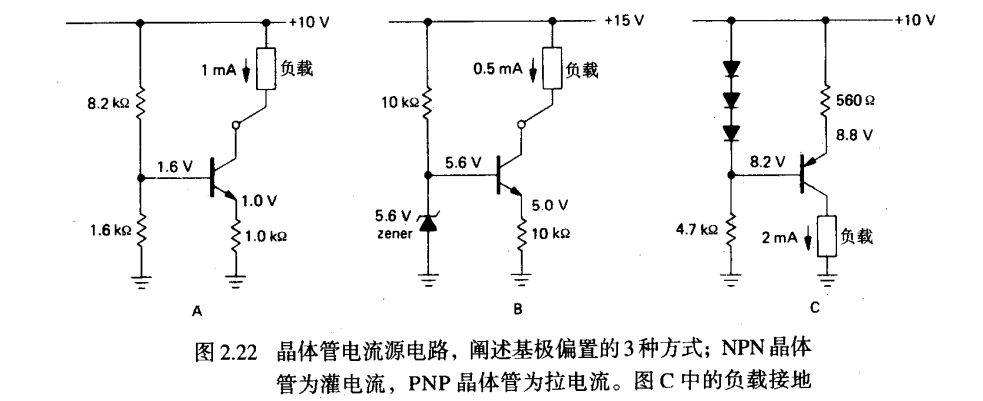
普通电流源电路
🖼️负载接地接法 负载接电源接法(高侧,低侧) 以及多种偏置方式
原理: 若将RLR_L直接用作RER_E,则变成一个一个电流源
非理想电流源因素
热效应(-2mV/℃)
Early Effect(ΔVBE=−0.0001ΔVCE\Delta V_{BE}=-0.0001\Delta V_{CE}) 万分之一
改进措施
...
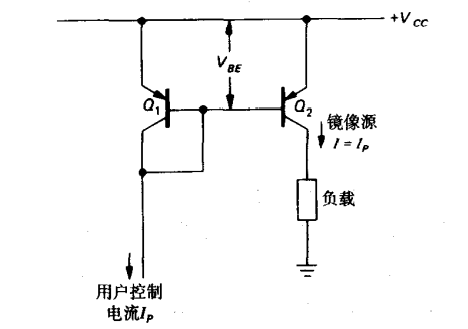
镜像恒流源
直接连接
🖼️镜像电流源电路图
由于Early效应(ID随VCEI_D随V_{CE}变化),其输出并非理想电流源
厄利效应: 小电阻信号,会有偏移?
Wilson电流源
通过二极管钳位,使得Q_1 Q_2的V_CE为恒定值
🤔VI分析法
从电源正极出发到电源负极
寻找一条可以确定值得回路
计算
稳压器
基本稳压管电路
三极管稳压电路
带反馈的三极管稳压电路
四.其他技巧
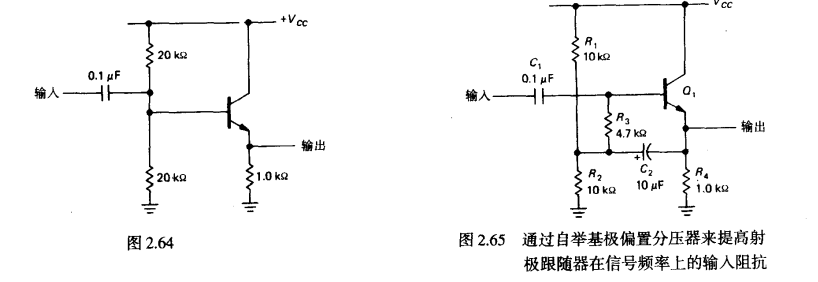
自举电路
获得更好的输入阻抗
💡通过将输入偏置的一部分转化为放大回路中的一部分,同时通过放大回路放大,使得阻抗变大
实际分析
🖼️自举电路分析图示
在无自举的时候,对于交流信号,ri=20K∣∣20K+1K∗βr_i=20K||20K+1K*\beta,是简明的
在加入自举后,C2C_2相当于导线,,由于跟随器Vb=VeV_b=V_e,相当于导线将R_3短路了
一般来说,将一个器件短路了,电阻会下降
精妙之处在于,将R3R_3短路后R1R_1,R2R_2从Base-Ground的电阻转变为了,Emitter-Ground的电阻,其对输入电阻的贡献需要考虑放大效应
自举后ri=(R4∣∣10K∣∣10K)∗βr_i=(R_4||10K||10K)*\beta
🤔总结
跟随器效应构造电压相等,使得跟随器输入输出之间的回路没有电流构造"虚断"
电容构造交流效应
实现输入偏置转化为放大回路的一部分
AB类推挽输入的自举实例
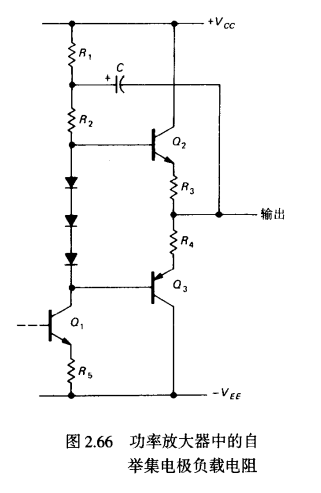
🖼️AB类推挽输入的自举实例
达林顿连接/Sziklai连接
达林顿(类似NPN)
导通电压为2个二级极管压降
饱和电压为1个二极管压降(考虑VC>VB1V_C>V_{B_1},而VB1V_{B_1}和VB2V_{B_2}相差一个压降)
优点:
提高了放大倍数
缺点
速度变慢,Q_1不能很快得切断Q_2
漏电流问题:
如果关闭即Q_1关闭,从Q_1分析,相当于CE间有个大的电阻,可能有为小的漏电流导致Q_2开启
小信号放大器漏电流为nA 功率管典型值为几百μA\mu A
改进: Q_2 BE之间并联电阻
提高控制速率?
加入电阻R防止上述发生,使得想要导通Q_1,也必须导通R
而R所需电流几乎不变为0.6/R,对漏电流而言,这个值足够大防止漏电流导通,
对于放大模式而言,这个值又太小,不影响放大倍数
电阻典型值 功率管为几百Ω\Omega  小信号管为几千Ω\Omega
Sziklai连接(类似PNP)
导通电压仅为1个二级极管压降
饱和电压也为1个二极管压降,推导同上