量子力学

量子力学

一.波粒二象性

光电效应

定义: 当光照射在金属板上,有电子溢出的的现象

规律

f一定,光电子数正比于光强

经典: 光时电磁波,光强越大

光电子初动能与f成正比,无关光强

经典: 只要光强够大,无论何种频率都行

仅V>V_0时才有光电子

光子需要一定时间

爱因斯坦

光子概念: 光为以c运动的粒子流

光电效应: 光子被吸收时,一方面提供逸出能 一方面提供初动能

完美解释三个规律

康普顿

定义: X射线石墨闪射中 发现散射线与入射线的相同的波长成分外 还有更长的成分 且 与入射线波长 物质 无关 仅和 角度有关

经典理论: 入射光线进入,带点粒子受迫振动 散射频率等于入射频率 与实验不符

光子理论:

物理模型: 光子 和 静止电子 的弹性碰撞 X光子能量 10^4-10^5 eV 电子为数个eV

碰撞→光子能量传递电子→光子能量下降→频率下降波长变长

方程: 能量守恒 动量守恒 电子质量需满足相对论效应

结论: 同实验吻合

\Delta \lambda = \frac{h}{m_0c} ( 1-cos\phi )

意义

动量 动能守恒微观上成立

光子理论 相对论 的正确性

实物粒子波粒二象性

德布罗意假设:

德布罗意关系式: E=hνp=hλ=hmvE = h\nu \quad p = \frac{h}{\lambda} = \frac{h}{mv}E=hνp=λh​=mvh​﻿ 

若v<<cv<<cv<<c﻿,则有m=m0m = m_0m=m0​﻿

若v>>cv>>cv>>c﻿,则有
m=γm0m = \gamma m_0 
m=γm0​﻿
其中
γ=1/1−v2c2\gamma=1/\sqrt{1-\frac{v^2}{c^2}}γ=1/1−c2v2​​﻿

物质波: 与实物物质相联系的波

波尔氢原子

实验基础: 

无法描述谱线问题 有经验公式(Balmer) ν=RHC(122−1n2)\nu = R_HC(\frac{1}{2^2}-\frac{1}{n^2})ν=RH​C(221​−n21​)﻿ 

RHR_HRH​﻿为Rydberh常数 C为光速

扩展为ν=RHC(1n2−1n2)\nu = R_HC(\frac{1}{n^2}-\frac{1}{n^2})ν=RH​C(n21​−n21​)﻿

经典理论: 电子绕核运动→辐射电磁波→半径减小→原子坍塌 且电磁波需连续

波尔假设

原子系统只能处在不连续能量状态 称稳定状态

角动量为J = nh

量子角动量

电子绕原子核运动,半径为rrr﻿

相当于形成驻波 且有
 2πr=nλ=nh/p=nh/mv2\pi r = n\lambda = nh/p = nh/mv2πr=nλ=nh/p=nh/mv﻿

化简得L=rmv=nh/2πL=rmv=nh/2\pi  L=rmv=nh/2π﻿ n取正整数 即量子角动量条件

推导

戴维孙-革末电子衍射实验

实验内容: 散射器电流出现周期变换

解释: 将电子看成波 满足λ=hp=h/2m0eU\lambda = \frac{h}{p} = h / \sqrt{2m_0eU}λ=ph​=h/2m0​eU​﻿ 
          当波长需满足如下条件时候 nλ=2dsinϕn\lambda = 2dsin \phinλ=2dsinϕ﻿ nnn﻿取整数时得最大电流III﻿

           联立得U=nh2dsinϕ2em0=nC\sqrt{U} = n \frac{h}{2dsin \phi \sqrt{2em_0}} = nCU​=n2dsinϕ2em0​​h​=nC﻿

GP汤姆孙实验

内容: 600eV慢电子射向铝箔,得到类似X射线得衍射图像

约恩孙实验

内容: 电子单缝 双缝 三缝 衍射实验

应用:

电子显微镜

隧道扫描仪

结论

既不是经典粒子 也不是经典波

经典波: 

光的粒子性总结

光的能量: ϵ=hν=mc2=m0c21−v2c2 \epsilon = h \nu = mc^2 = \frac{m_0c^2}{\sqrt{1-\frac{v^2}{c^2}}}ϵ=hν=mc2=1−c2v2​​m0​c2​﻿

由相对论变化得最后一个表达式

对于光子,若想使得最后一个表达式有意义,则m0m_0m0​﻿必然为0(无静质量)

光的质量: m=ϵc2=hνc2m = \frac{\epsilon}{c^2} =\frac{h \nu}{c^2}m=c2ϵ​=c2hν​﻿

光的动量: p=mc=ϵc2c=hvc=hλp = mc = \frac{\epsilon}{c^2} c = \frac{hv}{c} = \frac{h}{\lambda}p=mc=c2ϵ​c=chv​=λh​﻿

其中ϵ m p\epsilon \  m \ pϵ m p﻿ 表现粒子性 h ν λh\  \nu \ \lambdah ν λ﻿ 表现波动性

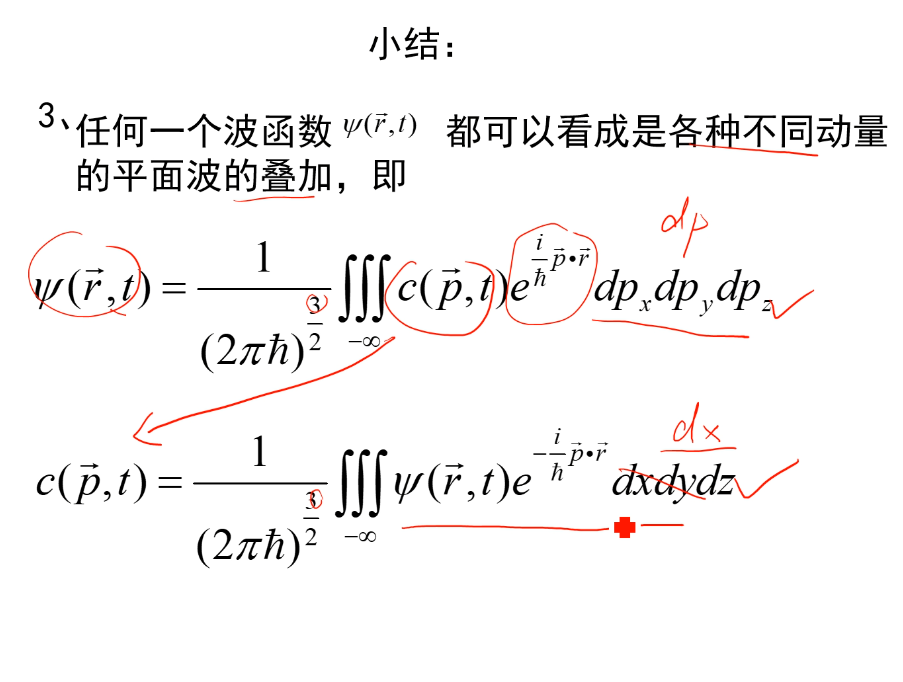
波函数

理论思路: 类比光 从电子波动性出发 以概率统计得方式解释了波函数得物理意义

                 衍射波波幅用Φ(r⃗,t)\Phi(\vec{r},t)Φ(r,t)﻿ 衍射花样强度用∣Φ(r⃗,t)∣2|\Phi(\vec{r},t)|^2∣Φ(r,t)∣2﻿ 但强度表示出现的概率

实验基础: 干涉实验电子波动性 为 语段电子叠加的统计结果

类别: 光强大: 光波振幅大 光子出现几率大 物质波大: 波函数振幅大 单个粒子出现几率大

量子力学第一假设: 波函数再空间某点的强度与在这点找到粒子的几率成正比

波函数标准化条件

dw(r⃗,t)=c∣Φ(r⃗,t)∣2dτdw(\vec{r},t)=c |\Phi(\vec{r},t)|^2 d\taudw(r,t)=c∣Φ(r,t)∣2dτ﻿ dτd\taudτ﻿为体积元 dw(r⃗,t)/dτdw(\vec{r},t)/d\taudw(r,t)/dτ﻿ 为 www﻿几率密度

出现概率仅取决于相对强度,而非绝对强度(归一化表示的函数值)

有限性: dwdwdw﻿积分一定为有限值→波函数绝对值平方可积→若不可及则c趋于0(可对其归一化)

单值性: 任意概率密度任意时刻确定的

连续性: 由势场性质

态叠加原理

P=∣Ψ1+Ψ2∣2=Ψ12+Ψ12+∣Ψ1Ψ2∗+Ψ1∗Ψ2∣=P1+P2+干涉项P=|\Psi_1+\Psi_2|^2=\Psi_1^2+\Psi_1^2+|\Psi_1\Psi_2^*+\Psi_1^*\Psi_2| = P_1 + P_2 + 干涉项P=∣Ψ1​+Ψ2​∣2=Ψ12​+Ψ12​+∣Ψ1​Ψ2∗​+Ψ1∗​Ψ2​∣=P1​+P2​+干涉项﻿

若放置探测器通过缝时,波函数坍缩,干涉条纹小时

叠加态原理: 若Ψ1Ψ2...Ψn\Psi_1 \Psi_2 ... \Psi_nΨ1​Ψ2​...Ψn​﻿为体系一个状态 则其线性叠加也是一个状态叠加常数为复数

注意是态的线性叠加而非概率的线性叠加

薛定谔的猫的解释: 宏观体系不允许存在一个由多个态线性叠加的态

低能电子衍射射线镍111面实验

实验内容: 用不同电流计收集器不同衍射角的动能

理论:

镍衍射解析和例题

结论: 任意一个波函数可以看作不同平面波的叠加

拉氏变换的公式

二.能量量子化

热辐射

定义: 任何物体在任何温度向空间辐射电磁波

规律: 

辐射能量 辐射能量的波长分布 同 温度相关

一部分反射 一部分吸收 但不同物体吸收能力不同

辐射本领越大 吸收能力也越大

解释: 原子无规则热运动中 碰撞 原子激发 热辐射 热运动与温度有关 故热辐射同温度相关

平衡热辐射定义: 物体既向外热辐射 也 吸收热辐射 当二者平衡保持温度不变 

黑体:

物理模型: 通过空腔开小洞,使得辐射进入后难以逃出

理想黑体吸收率为1 也是 理想的辐射体

规律: 热平衡时 黑体能量密度和辐射波长分布曲线仅和温度相关,而和形状材料无关 

经典物理学工作

韦恩公式: 经典热力学 麦克斯韦速度分布律 短波段符合

瑞利-金斯: 经典电磁 能量均分导出 长波段符合 但短波段公式不收敛 成为紫外灾难

普朗克量子化

模型:

空腔内分子原子看作带点的一维谐振子,辐射电磁波,并和电磁场交换能量

但是谐振子能量需量子化.其能量子为ϵ=hν\epsilon = h\nuϵ=hν﻿,对于频率为ν\nuν﻿的电磁波,只能以该频率能量子的整数倍吸收和发送

结论:

...

v很小时,还原成韦恩

v很大...

意义:

解决黑体理论基本问题

标志量子力学得诞生

三.薛定谔方程

量子力学核心问题

由于量子状态由波函数描述,波函数确定其任意力学量也确定

波函数满足的动力学学方程

求解各种体系下的动力学方程,得到随时间演化的波函数

态随时间变化的方程要求(类比经典力学中求取牛顿定律方程)

方程是线性: 态叠加原理要求

方程系数不含状态参量: 若含,体系状态只能部分满足方程

t x y z均为变量 偏微分方程

含有普朗克常数

推导

薛定谔方程推导

当U不含时间t,可化定态薛定谔方程

意义

基本假设(无法从理论严格推导)

反应微观粒子运动规律

定态薛定谔

波动薛定谔(外场存在下)

iℏ∂∂tΨ(r,t)=[−ℏ22μ∇2+V(r)]Ψ(r,t)i\hbar \frac{\partial}{\partial t} \Psi (r,t) = [-\frac{\hbar^2}{2\mu}\nabla^2 + V(r)]\Psi (r,t) iℏ∂t∂​Ψ(r,t)=[−2μℏ2​∇2+V(r)]Ψ(r,t)﻿

令Ψ(r,t)=Ψ(r)f(t)\Psi (r,t) = \Psi (r) f(t) Ψ(r,t)=Ψ(r)f(t)﻿ψ(r)\psi (r)ψ(r)﻿为空间波函数f(t) f(t)f(t)﻿为时间波函数

带入1式

iℏψ(r)ddxf(t)=f(t)[−ℏ22μ∇2+V(r)]Ψ(r)i\hbar \psi(r) \frac{d}{dx} f (t) =f(t) [-\frac{\hbar^2}{2\mu}\nabla^2 + V(r)]\Psi (r)  iℏψ(r)dxd​f(t)=f(t)[−2μℏ2​∇2+V(r)]Ψ(r)﻿

同除Ψ(r)f(t)\Psi (r) f(t)Ψ(r)f(t)﻿,参数分离

iℏ1f(t)ddxf(t)=1ψ(r)[−ℏ22μ∇2+V(r)]ψ(r)=Ei\hbar \frac{1}{f(t)} \frac{d}{dx} f (t) = \frac{1}{\psi(r)} [-\frac{\hbar^2}{2\mu}\nabla^2 + V(r)]\psi (r) = Eiℏf(t)1​dxd​f(t)=ψ(r)1​[−2μℏ2​∇2+V(r)]ψ(r)=E﻿

对于iℏddxf(t)=Ef(t)⇒f(t)=ce−iEt/ℏi\hbar  \frac{d}{dx} f (t) = Ef(t) \Rightarrow f(t)=ce^{-iEt/\hbar}iℏdxd​f(t)=Ef(t)⇒f(t)=ce−iEt/ℏ﻿ (一阶偏微分)

而有Ψ=ψ∗e−iEt/ℏ\Psi=\psi * e^{-iEt/\hbar}Ψ=ψ∗e−iEt/ℏ﻿

接下来求解[−ℏ22μ∇2+V(r)]ψ(r)=Eψ(r) [-\frac{\hbar^2}{2\mu}\nabla^2 + V(r)]\psi (r) = E\psi(r) [−2μℏ2​∇2+V(r)]ψ(r)=Eψ(r)﻿此式子也称定态薛定谔方程 需要联立边界调节解出ψ(r)\psi(r)ψ(r)﻿

分析

波函数和时间t为正弦关系 ω=E/ℏ\omega = E/\hbarω=E/ℏ﻿

由德布罗意关系的E就是波函数Ψ\PsiΨ﻿所描述的能量,也就是说,能量为常数,故称定态

几率密度和时间无关

几率ωn(r,t)=Ψn∗Ψn=ψ∗e−iEt/ℏψ∗eiEt/ℏ=ψ∗ψ\omega_n(r,t) = \Psi_n^* \Psi_n = \psi * e^{-iEt/\hbar} \psi * e^{iEt/\hbar} = \psi^* \psiωn​(r,t)=Ψn∗​Ψn​=ψ∗e−iEt/ℏψ∗eiEt/ℏ=ψ∗ψ﻿

几率流密度和时间无关

几率流密度推导

能量本征方程

能量算符推导

总结

PPT-定态波函数求解总结

定态波函数满足要求

一维无限深势阱

问题背景: 

金属中自由电子运动,由于势能影响,被限制在有限的范围,称之为束缚态

作为近似,认为其在一维无线深势阱中运动,即

函数-一维无限深势阱

推导

推导

波函数时空变化

概率守恒定律

推导

设\Psi

则有概概率密度w=\Psi^* \Psi

对时间求导(\Psi 已知: 薛定谔放长)

∂w∂t+∇J⃗=0\frac{\partial w}{\partial t} + \nabla \vec{J}= 0∂t∂w​+∇J=0﻿ (概率守恒方程 微分形式)

求体积积分, 应用高斯定理体积分转为面积分

所需条件 

概率密度和概率流密度w J必须连续→\Psi一阶连续

\Psi全空间可积→有限

综上 \Psi必须有限且连续且具有连续微商(一阶连续)

w应该为\vec{r} 和 t的单值函数

质量守恒定律

同时乘上m ∂wm∂t+∇Jm⃗=0\frac{\partial w_m}{\partial t} + \nabla \vec{J_m}= 0∂t∂wm​​+∇Jm​​=0﻿

质量流的定义和方程推导

电荷守恒定律

同时乘上q,方法同上

有限深对称方势阱

推导