八.线性时间排序

八.线性时间排序

一.比较排序复杂性的下界

排序决策树

术语约定:

序列: 区别于集合,这个容器还包含了不同元素的位置信息(不需要按元素大小排列)

定义输入序列: A[1] , A[2] , A[3] 记作 <1,2,3>此处以3个元素举例

则有排序后序列 我们定义为 π\piπ﻿[1] π\piπ﻿[2] π\piπ﻿[3] = Sort( A[1] , A[2] ,A[3] )  = Sort<1,2,3> = ?

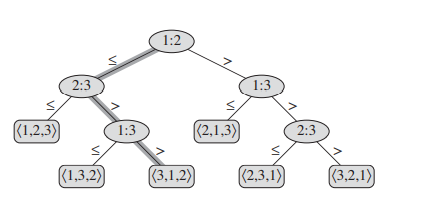
决策树分析

对于不同的输入序列 Sort<1,2,3> 可能有n! 个输出是<1,2,3>的所有排列.每一个输出对应一个叶节点(区别于Root节点,一般节点)

到达一个叶节点,相当于从决策树上从上往下走,经过的层数为比较次数

有n!个叶节点 ⇒ 为 2TreeHigh≥n!(if Blance)2^{TreeHigh} \geq n!\quad (if\ Blance)2TreeHigh≥n!(if Blance)﻿ ⇒ TreeHigh=h≥log⁡2(n!)=Ω(nlgn)TreeHigh=h\geq\log_2{(n!)} = \Omega(nlgn) TreeHigh=h≥log2​(n!)=Ω(nlgn)﻿

二.计数排序

算法实现

代码

Count-Sort(A,MaxNum)
{
	Let Buf[1..A.Length] new array
	Let Count[1..Dict.MaxNum] new array

	init i = 1;
	for i = 1 to A.Length
		Count[A[i]] ++
	for i = 1 to Count.Length
		C[i] C[i] + C[i-1]

	for i = 1 to A.Length
		Buf[ Count[A[i]] ] = A[i]
		Count[A[i]] ++

	return Buf
}

Copy

算法分析

新建缓存数组Buf(非原址排序) 和 计数数组Count

遍历A,在对应的Count中表上记号( Count[A[i]]++ )

遍历Count,将Count计算为Sum_Count求和数列.求取A[i]在Buf中对应的offset

遍历A[i],根据Count[A[i]]中的偏移量拷到Buf中,Buf[ Count[A[i]] ] = A[i]

算法思考

指针数组: 这里的Count数组实际上就是一个Index数组(指针数组)

缺点是显而易见的,根据MaxNum(数据的范围)决定Count数组大小,可能会消耗大量的空间

三.基数排序

算法实现

代码

Radix-Sort (A,d)
{
	for i = 1 to d
	 use a stable sort to sort on dig i 
}

Copy