三.频域分析

频域分析基础

原理

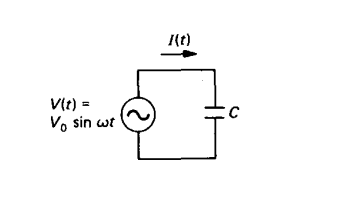
某个f频率的激励,经线性电路,输出也为f频率(相位 幅度改变)

线性电路: 具有叠加性

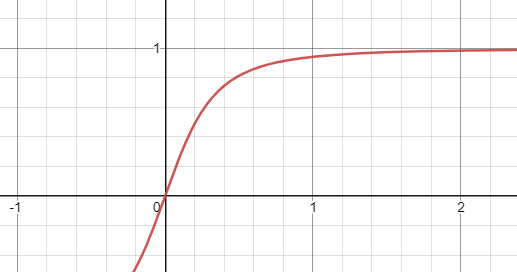
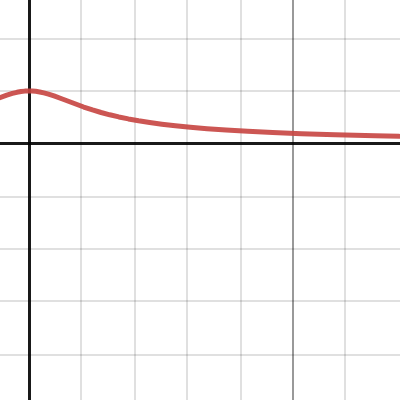
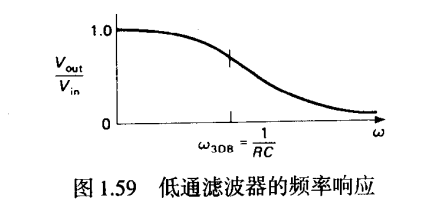
故只需研究单一频率输入和其对应输出,可绘制频率响应图

通过时域分析频域(经典解方程)

电抗电路原理图

则有I=CdVdt=CV0ωcos⁡ωtI=C\frac{dV}{dt}=CV_0\omega \cos\omega tI=CdtdV​=CV0​ωcosωt﻿

不考虑幅度则有增幅I=CωV0 I = C\omega V_0I=CωV0​﻿

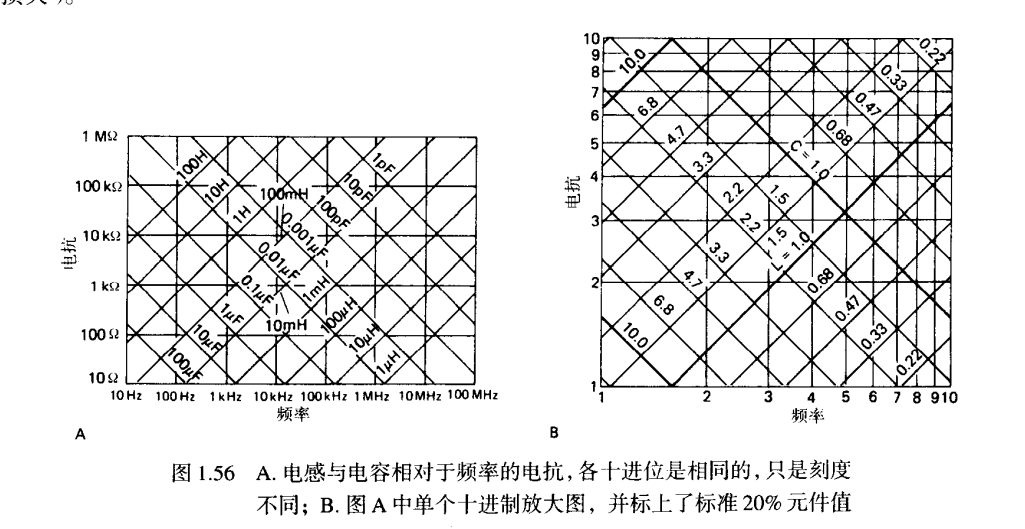
电抗为V0/I=1/CωV_0/I=1/C \omegaV0​/I=1/Cω﻿

相位分析法-带频率的相量分析

定义: 用复数的模表示增幅 用复数的幅角表示相位

为何这里不采用ejwt+ϕe^{jwt+\phi}ejwt+ϕ﻿的形式连频率一起考虑?

本质上是可以的,但没有必要

考虑三角函数的正交性,不同频率的电压*电流其平均功率一定为0

通过取相位的实部来得到原来的表达式

则有电容阻抗 Z=1ωCj=−jωCZ=\frac{1}{\omega C j}=\frac{-j}{\omega C}Z=ωCj1​=ωC−j​﻿

电抗功率分析

P=1T∫0TV(t)I(t)dt=Re(VI∗)P=\frac{1}{T}\int_{0}^{T}V(t)I(t)dt=Re(VI^*)P=T1​∫0T​V(t)I(t)dt=Re(VI∗)﻿

①P=1T∫0TV(t)I(t)dt①P=\frac{1}{T}\int_{0}^{T}V(t)I(t)dt①P=T1​∫0T​V(t)I(t)dt﻿

由于仅考虑正弦信号则有

V(t)=A_1cos(\omega_1t+\phi_1)=e^{(j\omega_1t+\phi_1)}+e^{-(j\omega_1t+\phi_1)} /2\\ I(t)=A_2cos(\omega_2t+\phi_2)= e^{(j\omega_2t+\phi_2)}+e^{-(j\omega_2t+\phi_2)} /2\\ 带入表达式①\\ 得表示式,若允许使用Re()运算符则有\\ P=\int_0^TRe(VI+VI^*)

若f1≠f2f_1≠f_2f1​=f2​﻿则有正弦正交性得两项为0

若f1=f2,VIf_1=f_2,VIf1​=f2​,VI﻿依旧为0,但VI∗VI^*VI∗﻿为一个常向量,Re(VI∗),Re(VI^*),Re(VI∗)﻿可能不为0

故只需要考虑VI∗VI^*VI∗﻿即可

显然有Re(VI∗)≤∣V∣∣I∣Re(VI*)≤|V||I|Re(VI∗)≤∣V∣∣I∣﻿ ,二者比值定义为功率因数Q=P∣V∣∣I∣ Q= \frac{P}{|V||I|}Q=∣V∣∣I∣P​﻿

Q取自0-1 取0时为纯电抗 取1时候为纯电阻

RC滤波器

忽略相位分析法

原理: 对于许多电抗分析,我们往往只关心频率响应图,不关心其相位(或者用经验公式分析)

高通滤波:

响应-频率 图像

RC滤波器频率阻抗分析图

https://www.desmos.com/calculator/oflxnh93hx

不同电阻-电容搭配和其对应的3db点频率

RC串联时候阻抗为Z总=R+(−jωC)Z_总=R+(\frac{-j}{\omega C})Z总​=R+(ωC−j​)﻿

则有R上电压为RR+(−jωC)V\frac{R}{R+(\frac{-j}{\omega C})}VR+(ωC−j​)R​V﻿

若考虑相位难以分析

若不考虑相位Z总=(R2+1(ωC)2)12∗ejθZ_总=( R^2+\frac{1}{(\omega C)^2})^{\frac{1}{2}}*e^{j\theta}Z总​=(R2+(ωC)21​)21​∗ejθ﻿

则有R上电压V=RZ总=R(R2+1(ωC)2)12∗ejθ2∗VV=\frac{R}{Z_总}=\frac{R}{( R^2+\frac{1}{(\omega C)^2})^{\frac{1}{2}}}*e^{j\theta_2}*VV=Z总​R​=(R2+(ωC)21​)21​R​∗ejθ2​∗V﻿

振幅为RωC((ωC)2R2+1)12∗Vin\frac{R\omega C}{(( \omega C)^2R^2+1)^\frac{1}{2}} * V_{in}((ωC)2R2+1)21​RωC​∗Vin​﻿

当ω=1RC即f=12πRC\omega = \frac{1}{RC} 即 f= \frac{1}{2\pi RC}ω=RC1​即f=2πRC1​﻿ 取 3db

低通滤波

响应-频率 图像

分析同上

最后有振幅1((ωC)2R2+1)12∗Vin \frac{1}{(( \omega C)^2R^2+1)^\frac{1}{2}} * V_{in}((ωC)2R2+1)21​1​∗Vin​﻿

谐振电路(带通滤波)

带通滤波器电路

响应-频率图

1/Z=jωC+1/jωL⇒Z=jωL1−ω2LC为打勾函数求双刀函数求倒数1/Z = j\omega C +1/j\omega L \Rightarrow Z = \frac{j\omega L}{1 - \omega^2 LC} 为打勾函数求双刀函数求倒数1/Z=jωC+1/jωL⇒Z=1−ω2LCjωL​为打勾函数求双刀函数求倒数﻿

理论上再f=12πLCf = \frac{1}{2\pi \sqrt{LC}} f=2πLC​1​﻿即ω=1LC  \omega = \frac{1}{ \sqrt{LC}} ω=LC​1​﻿时取得阻抗无穷大 

由于电容电感的损耗,达不到那么高的尖锐度 往往用品质因数QQQ﻿描述尖锐度

Q=f3dbf谐振Q=\frac{f_{3db}}{f_{谐振}}Q=f谐振​f3db​​﻿ 对于R+L||C电路而言Q=ω0RCQ=\omega_0 RC Q=ω0​RC﻿

 LC陷波电路

响应-频率 图像

Q=f3dbf syntony Q=\frac{f_{3db}}{f_{ \text{ syntony }}}Q=f syntony ​f3db​​﻿ 对于R+L||C电路而言Q=ω0L/RQ=\omega_0 L/RQ=ω0​L/R﻿