一.分治法的归并排序
分治法步骤
分解: 分解成若干个子问题
解决: 解决子问题,子问题足够小时候直接求解
合并: 合并子问题
归并排序算法分析
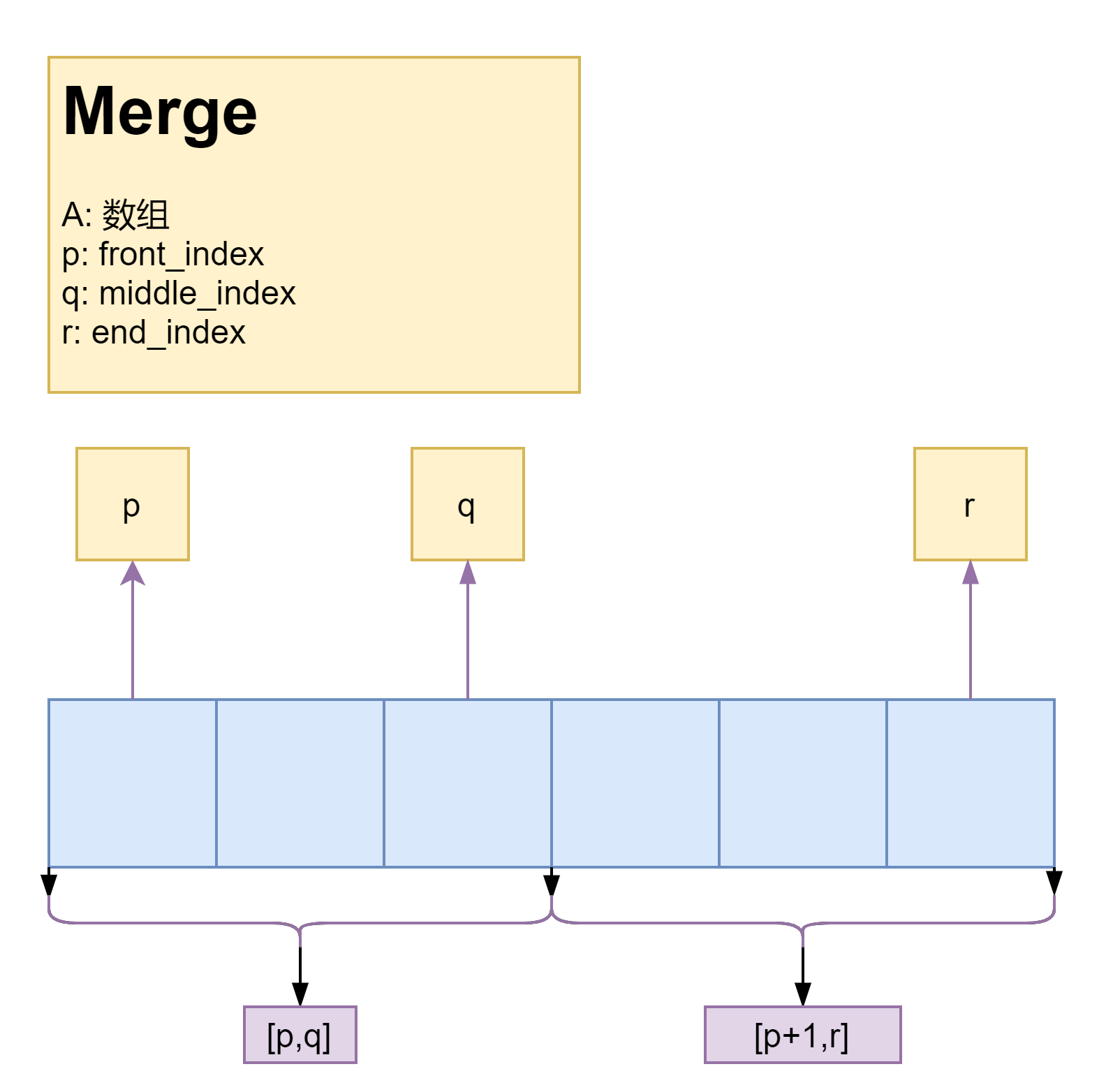
关键是合并(Merge)两个已排序的子序列
合并的基本思路是通过两个下标,逐项比较.
Merge 代码的实现
Merge(A , p , q , r)
n1 = q-p+1 (计算子序列n1长度)
n2 = r-(q+1)-1 (计算子序列n2长度)
Let L[1:n1+1] R[1:n2+1] become new arrays
(将两个子序列拷贝到缓冲区L(eft) R(ight)数组中)
copy A[p:q] to L[1:n1]
copy A[q+1:r] to R[1:n2]
(设置哨兵元素,供接下来的比较标识行尾)
L[n1+1] = infinite
R[n2+1] = infinite
init i1 = 1, i2 =1 ;(建立指针index)
for(init k = p; k==r ; k++)
{
if L[i1]<R[i2] then { A[k]=L[i1]; i1++}
else then { A[k]=R[i2]; i2++}
}
Copy
C++
Merge-Sort (A , p , r)
{
if(p == r) then { return } (直接相当于排序好了)
else
{
q = ⌊ p+q/2 ⌋ (向下取整)
Merge-Sort (A , p , q)
Merge-Sort (A , q+1 , r)
Merge(A,p,q,r)
}
}
Copy
C++
Merge 代码细节分析
计算子序列n1长度 n2长度
将两个子序列拷贝到缓冲区L[1:n1+1] R[1:n2+1]数组中
设置哨兵元素到多余的缓冲区末尾,供接下来的比较标识行尾
循环比较,将缓冲区内容按顺序搬运A
二.最大和的连续子序列
问题简介
整数序列A1,A2...An,寻找求合值为大的序列
穷举法(遍历法)
算法分析
设index [i,j] 用两个循环分别遍历所有的可能,一共有种可能
对每种可能求和并保存其中的最大值
算法复杂度分析(多层循环下的复杂分析示例)
若不保存子序列的结果,而是只记载最大的子序列,则有三层循环
两个index下标循环带来的下限
对于每个子序列,中,每一项代表外层循环的index不变(i) 内层循环的index变动
取的第一项: 代表着 对于每一对ij,内部需要次加法
第一项变化为,同理第二项变化为
遍历法的简单优化-算法分析
[star t: end]子序列求和,可以由上一次求和[start : end-1]的结果加上[end]得到
只需要二层循环可以分析得到算法
也可将每个结果保存在一个二位数组中,通过最后再来遍历这个二位数组的结果
不只最大最小值
极度消耗空间,所有的情况仅为 如果非连续情况下有情况无法分析
分治算法
算法分析
最大子数组位于A[low:mid]中→递归调用自身
最大子数组位于A[mid:high]中→递归调用自身
最大子数组横跨于数组的中间→执行的寻找最大子数组
则有 可通过主方法\递归树法证明
代码实现
Find-Max-CrossingMiddle-Subarray(A,low,mid,high)
{
{
查找左边[low:mid]最大子序列
init left-point = mid
init left-sum = A[mid]
init temp-sum = 0
for i = mid->low
temp-sum = sum + A[i]
if temp-sum > left-sum then {left-sum = temp-sum, left-point = i}
}
{
查找右边[low:mid]最大子序列,步骤一致忽略
}
{return left-point , right-point , right-sum + left-sum}
}
Copy
C++
Find-Maximum-Subarray(A,low,high)
{
if high == low then {return low,high,A[kow]}
else
{
(left-low,left-high,left-sum) = Find-Maximum-Subarray(A,low,high+low/2)
(right-low,right-high,right-sum) = Find-Maximum-Subarray(A,high+low/2,high)
(mid-low,mid-high,mid-sum) = Find-Max-Crossing-Middle-Subarray
}
{比较三个的返回mid-sum,left-sum,right-sum , 选择最大的一组参数返回即可}
}
Copy
C++
三.带入法求解递归式
代入法(数学归纳法)简介
本质上是一种严谨验证解的形式
需要先猜测解,然后再带入解,利用数学归纳法
带入法示例
确定的上界,猜测
则有
证明原猜测成立
数学归纳法的注意事项
注意必须严格成立
不能说所以成立
此处为数学归纳法证明,需要和归纳假设严格一致的形式,不能循环证明
数学归纳法的初始条件选择
我们需要证明的上界 对于不成立
但是渐进符号的定义也没有要求从就要成立,我们可以手动选择的n_0
实际上,上述示例中时候表达式即成立了
猜测解的选择技巧
考虑n取非常大的情况
比如示例
当n非常大时候 +17可以被忽略,于是结果还是
猜测解通过加减低阶项实现证明
考虑 猜测解为
带入则有 和猜测解不严格一致
但是发现只相差一个低阶项,高阶项的系数是正确的
不妨假设 带入即可解决问题
变量代换解决问题
求解 可通过 令
变换为 再令
得到
四.递归树法求解递归式
代入法的问题:
代入法可以简洁的证明一个递归式的猜测解,但本身无法得到猜测解
此时可以用递归树方法解决,但是要忍受一些不精确
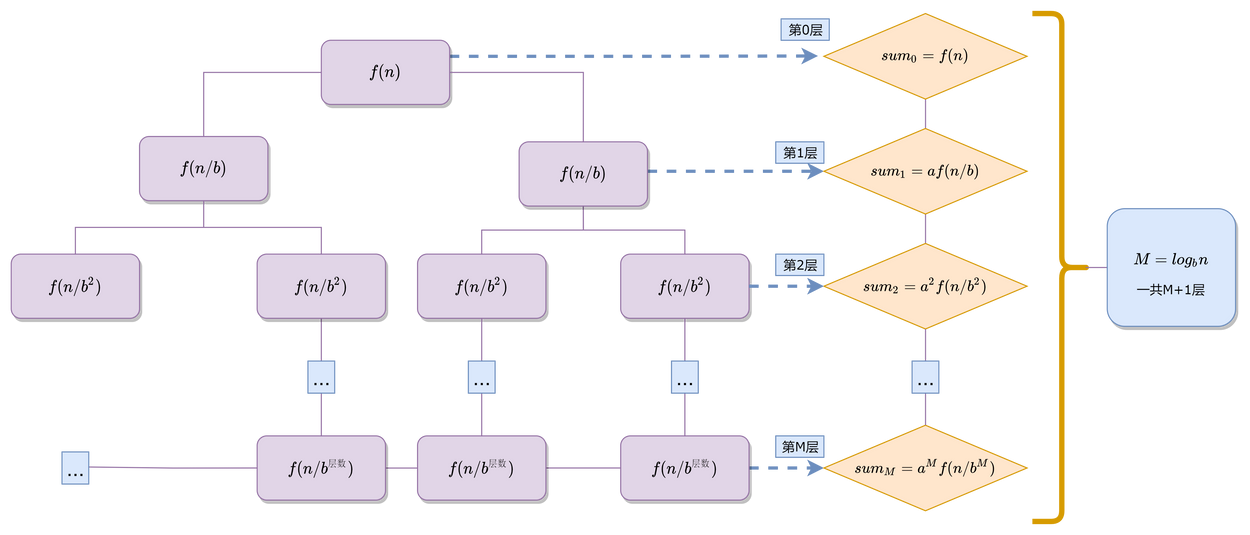
对于任意的 一些参数定义
从第0层到第M层,一共M+1层
s 用m表示具体第几层,M表示m的最大层
例子
五.主方法求解递归式
主方法内容
其中n/b解释为或
比较 和 渐进大小区别
我法-主定理证明
即求
当时候
求和证明
可以看见分母,关键是比较 的渐进大小
问题1: 当二者渐进相等的时候,本求和无法说明为何
解决,当二者渐进相等,每一项 均为 不再可以使用等比求和公式替代,直接即可
标准证明方法