二.算法基础(Merge-Sort/Insert-Sort)

二.算法基础(Merge-Sort/Insert-Sort)

一.插入排序算法

问题简介

最古老的算法问题

输入<a1,a2, .... ,an>

输出<a1',a2', .... ,an'> 且有(Such that$) a1'≤a2'≤ .... ≤an'

插入排序原理分析

输入规模: 不同问题的定义不同,此处的度量为 项数nnn﻿

运行时间: 执行的基本操作的"步数"

如果While 或 for是正常退出的话(从while(...)判断语句退出)则判断语句本身执行次数比循环体多1次(基本可以忽略)

插入排序(Insert Sort)代码

插入伪代码(从小到大)

Insert_Sort(A)
for j=[2 -> A.Length]
	　key = A[j]
		i = j - 1
		while i between[1 , j-1] and A[i]>key
			A[i+1] = A[i]
			i = i- 1
		A[i+1] = key

Copy

JavaScript

代码时间分析

t2=c2∗(A.length−1)循环次数+1(for语句额外比较次数)t2 =c2* (A.length-1)_{循环次数}+1_{(for语句额外比较次数)}t2=c2∗(A.length−1)循环次数​+1(for语句额外比较次数)​﻿

t3+t4+t8=(C)∗(n−1)循环次数t3+t4+t8 = (C)*(n-1)_{循环次数}t3+t4+t8=(C)∗(n−1)循环次数​﻿

t5=∑i=n−1外部循环次数i=1(x)内部循环次数+1额外开销t5= \sum\limits_{i=n-1_{外部循环次数}}^{i=1} (x)_{内部循环次数} +1_{额外开销}t5=i=n−1外部循环次数​∑i=1​(x)内部循环次数​+1额外开销​﻿

其中有x取决于具体的数据输入,x最坏为i−1i-1i−1﻿,构成一个t5=n−1+n−2+n−3...+1+0=(n−1)n2t5= n-1 + n-2 +n-3 ... + 1 + 0 = \frac{(n-1)n}{2}t5=n−1+n−2+n−3...+1+0=2(n−1)n​﻿

t6+t7=∑i=n−1外部循环次数i=1(i−1)内部循环次数t6+t7 =  \sum\limits_{i=n-1_{外部循环次数}}^{i=1} (i-1)_{内部循环次数}t6+t7=i=n−1外部循环次数​∑i=1​(i−1)内部循环次数​﻿

代码细节解析

保存目前的 将要被排序位 A[Key], 范围为[2,A.length]

为何从2开始? 设Key=n,能使用如上循环的的条件为A[1:n-1]有序,A[1:1]有序这是显然成立

A.length == 1的情况?

将 Key位 的前一位作为 比较位A[i]

比较A[i]和A[key]

A[i]>A[key] : 向后搬移一位 i=i-1 再次循环

A[i]<A[key] : 向后搬移一位 A[i]=A[key]

While的If形式理解: While程序体内相当于if,满足条件即执行.外加一个强制比较的环节,程序题外相当于else

具体的逻辑判断: 考虑 顺序逆序排序,考虑搬移方向

二.循环表达式证明

插入排序

假设我们以A[1:j]是否有序作为循环表达式的判定条件

起始: A[1:1]显然有序

循环: 若A[1:j-1]有序经过循环后可证明A[1:j]也是有序的

结束: 结束时候j=A.length 等价于 A[1:A.length]有序

以不同角度看待循环表达式的判定条件,就有不同的排序算法. 此处为子数组有序为依据,若将初始子数组划为均等划分,而不是只考虑A[0:1]则有归并排序的迭代方式

三.分治法的归并排序

分治法步骤

分解: 分解成若干个子问题

解决: 解决子问题,子问题足够小时候直接求解

合并: 合并子问题

归并排序关键

关键是合并(Merge)两个已排序的子序列

为何不需要单独排序算法,合并的时候,已经带有了比较操作,比如两个长度为1的子序列,合并他们等价于比较二者大小

合并的基本思路是通过两个下标,逐项比较.

同时可以加入一个无限大的哨兵元素表示到达子序列的末

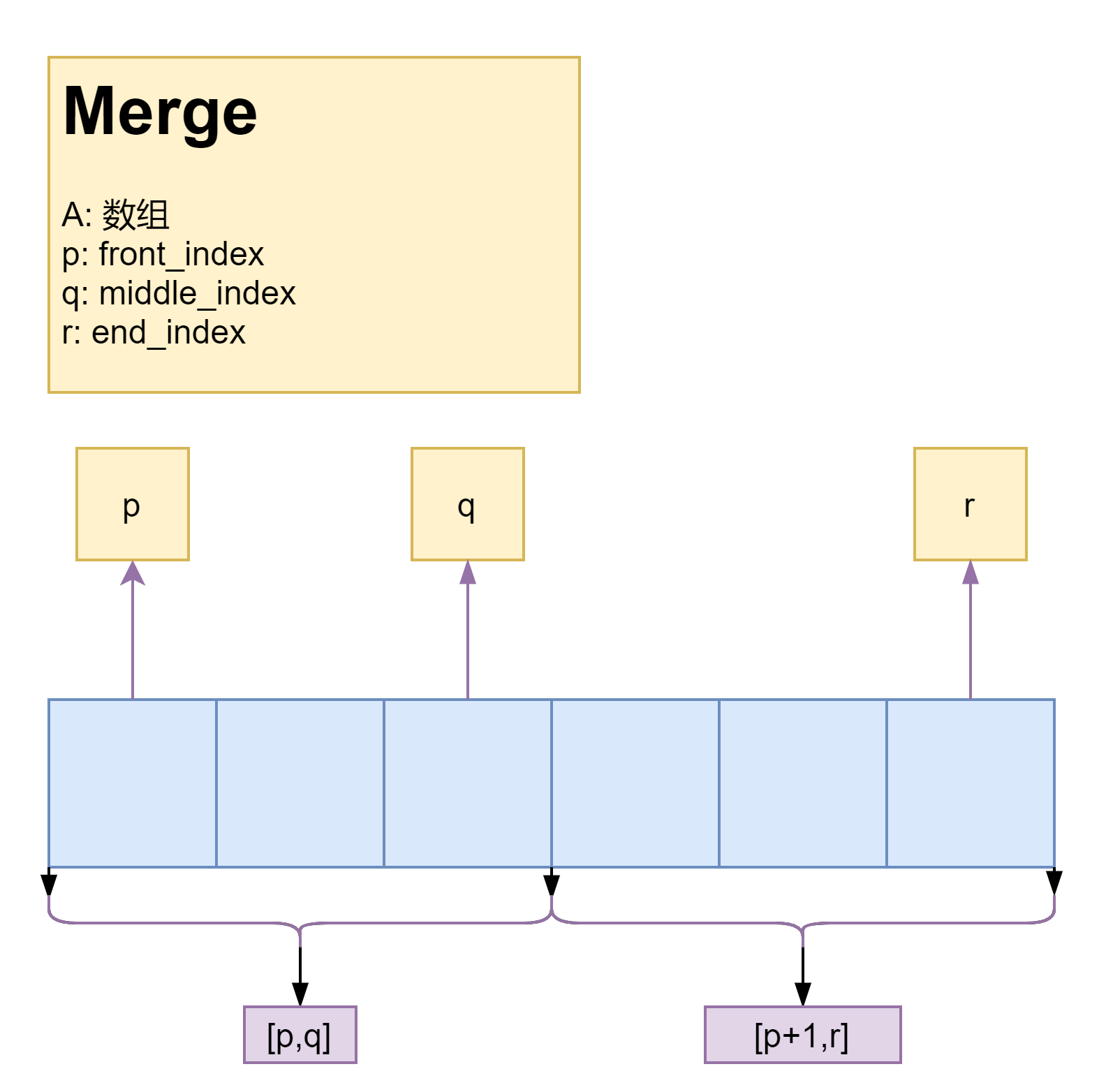
Merge 的实现

Merge API图示

归并伪代码

Merge(A , p , q , r)
	n1 = q-p+1 (计算子序列n1长度)
	n2 = r-(q+1)-1 (计算子序列n2长度)

	Let L[1:n1+1] R[1:n2+1] become new arrays 
	(将两个子序列拷贝到缓冲区L(eft) R(ight)数组中)
	copy A[p:q] to L[1:n1]
	copy A[q+1:r] to R[1:n2]
	
	(设置哨兵元素,供接下来的比较标识行尾)
	L[n1+1] = infinite
	R[n2+1] = infinite
	
	init i1 = 1, i2 =1 ;(建立指针index)
	for(init k = p; k==r ; k++)
	{
		if L[i1]<R[i2] then { A[k]=L[i1]; i1++}
		else           then { A[k]=R[i2]; i2++}
	}

Copy

C++

归并排序Merge-Sort伪代码

Merge-Sort (A , p , r)
{
	if(p == r) then { return } (直接相当于排序好了)
	else
	{
		q =  ⌊ p+q/2 ⌋  (向下取整)
		Merge-Sort (A , p , q)
		Merge-Sort (A , q+1 , r)

		Merge(A,p,q,r)
	}
}

Copy

C++

Merge 代码分析

计算子序列n1长度 n2长度

将两个子序列拷贝到缓冲区L[1:n1+1] R[1:n2+1]数组中

设置哨兵元素到多余的缓冲区末尾,供接下来的比较标识行尾

循环比较,将缓冲区内容按顺序搬运A